Ossos i geometries no euclidianes (2)

 A l'article anterior (Ossos i geometries no euclidianes-1) vam plantejar un conegut problema amb un enunciat semblant a aquest:

Un os camina un quilòmetre cap al sud seguint un meridià. Gira cap a l'oest i camina un altre quilòmetre seguint un paral·lel. Gira cap al nord i camina un altre quilòmetre seguint un meridià. Al final es troba al punt de partida. De quin color és l'os?

Vam veure que hi havia dos tipus de solucions. Un model amb infinites solucions a l'hemisferi sud del nostre planeta i un altre de més evident a l'hemisferi nord: el punt de sortida i arribada seria el Pol Nord. Vam observar al Pol es formava un triangle amb una suma d'angles interiors de més de 180º. Això no és possible al pla però sí a una superfície esfèrica. Va ser l'excusa per entrar en el mon de la geometria esfèrica, un dels tipus de geometries no euclidianes. En aquest article canviarem les superfícies sobre les que caminarà el nostre os i serà la porta d'entrada a un altre exemple de geometria no euclidiana: la hiperbòlica.

Imaginem al nostre os caminant sobre un paraboloide hisperbòlic. Aquesta superfície la podem trobar en les patates Pringles o, més sanament, en una superfície reglada com la que mostren al MMACA per a il·lustrar la multiplicació d'enters en 3D. Observarem que el recorregut de l'os és impossible perquè, deixant de banda la definició exacta de nord i sud, els meridians van sent divergents a mesura que es van separant del que podríem considerar com a zona equatorial.

Proposem el problema a una nova superfície: una pseudoesfera o tractricoide. Aquesta superfície, com l'anterior és infinita. És a dir, les "puntes" no acaben convergint sinó que són asimptòtiques. A l'hemisferi sud tenim, com a l'esfera, infinites solucions. Però al nord no en tenim cap perquè els meridians no convergeixen mai, només es van acostant cada vegada més.

Pseudoesfera i ruta en detall

Les dues superfícies presentades son molt interessants en sí mateixes. Però no ens toca estudiar-les ara. Les hem triat perquè son dos dels models físics de la geometria hiperbòlica, una geometria que tampoc acompleix el 5è postulat d'Euclides, però de forma diferent a les que havíem vist: al pla dèiem que "per un punt extern a una recta només passa una paral·lela a aquesta", i a l'esfera que "per un punt exterior a una "recta esfèrica" no passa cap paral·lela a aquesta". A la geometria hiperbòlica diem que:

Per un punt exterior a una recta hiperbòlica passen, com a mínim, dues rectes que són paral·leles a aquesta.

L'expressió "com a mínim dues", implica que poden ser infinites.

Com vam fer a l'article anterior haurem de redefinir algunes coses com "recta", "angle", "distància", "triangle"... i, a partir d'aquestes redefinicions, veure com podem conduir un debat a l'aula sobre aspectes com la relació amb els postulats euclidians,la suma dels angles interiors d'un triangle, com es calcula la seva àrea, com són les circumferències... No es tracta de fer un estudi a fons sinó de fer un primer contacte, d'aproximar-se a algunes idees generals. I tot amb dues raons de fons:

• comprendre millor el sistema axiomàtic de les matemàtiques. I, en concret, millorar la comprensió del proposat per Euclides fent una mena "d'estranyament", a base de modificar les seves regles i "moure'ns" en un món diferent.
• aproximar-nos a la revolució matemàtica que va suposar l'aparició de les geometries no euclidianes.

Aquesta geometria és més difícil d'estudiar amb materials. Podem imprimir algunes superfícies en 3D, però tampoc ens solucionarà gaire cosa, perquè és complex tot el que es relaciona amb la mesura. Aquí teniu un enllaç per a imprimir un paraboloide hiperbòlic i una pseudoesfera.

Hi ha alguns models plans de la geometria hiperbòlica. Per exemple, el model del Disc de Beltrami-Klien on el pla infinit es representa amb l'interior d'un cercle (la circumferència que el limita no en forma part) i les rectes per cordes d'aquesta circumferència. No entrem ara en el tema de les distàncies. La imatge mostra algunes de les moltes paral·leles a la recta a que passen pel punt P. Les que coincideixen amb la recta a  no la tallen perquè, com hem dit abans, la circumferència no forma part del disc.

Podeu trobar applets de GeoGebra per a treballar amb aquest model, però en aquest article optarem per un altre: el Disc de Poincaré. Pensem que aquest model és millor per treballar-lo a l'aula perquè les rectes no son segments rectilinis, com al model anterior, i la sensació "d'estranyament" serà més gran. Cal dir, però, que qualsevol model que agafem és més complicat que el de la geometria esfèrica, sobre la que podíem experimentar directament, i que té idees més intuïtives. Però si hem treballat la geometria de l'esfera prèviament, aquesta serà més fàcil d'acceptar. Serà com entrar a un món de videojoc amb unes regles diferents. I sobre el que podrem treballar amb GeoGebra ja que no és difícil trobar applets que ens permeten crear, manipular i mesurar objectes.

Límit circular III de M.C Escher (1959).
Aquesta obra està basada en el disc de Poincaré

Vols conèixer el món hiperbòlic amb idees per treballar-ho a l'aula?

Com és la vida al Disc de Poincaré?

Poincaré va descriure el seu disc relacionat amb índexs de refracció i temperatures. Però Martin Gardner, al llibre Damas, parábolas y más mistificaciones matemáticas,  opta per descriure'ns aquesta Planilàndia hiperbòlica d'una altra manera. Copiem íntegra la seva descripció:

"En l'enginyós model de Poincaré, cada punt del pla euclidià es troba en correspondència amb un punt situat a l'interior del cercle (però no sobre la seva circumferència). De l'altre costat de la circumferència l'únic que existeix és, com ha dit Escher, «el no-res més absolut».. 

Imaginem que aquest model està habitat per planilandesos. Així que vagin allunyant-se de centre ens anirà semblant que es fan progressivament més petits, encara que ells no detectaran la contracció del seu entorn, perquè els seus sentits i els seus instruments de mesura es van contraient en proporció idèntica. Si arribessin a la frontera, la seva grandària seria nul·la, però la frontera els és inaccessible. Si es dirigissin cap a ella amb moviment uniforme, nosaltres els veuríem desaccelerar progressivament, encara que als viatgers els hi semblaria que la seva velocitat és constant. Per tant, el seu univers, que nosaltres percebem finit, és infinit per als planilandesos. Els raigs de llum del món hiperbòlic es propaguen sobre línies geodèsiques, però com (per a nosaltres) la seva velocitat és proporcional a la distància de la frontera, els veuríem descriure arcs de circumferència que a l'aproximar-se al perímetre del disc tendeixen a tallar-lo en angle recte."

Com veiem les "rectes hiperbòliques" (que a partir d'ara anomenarem senzillament "rectes") són, majoritàriament, arcs de circumferència que son perpendiculars en els punts ideals on tallarien la circumferència del disc, que, recordem, no forma part d'aquest pla hiperbòlic. Les que uneixen dos punts diametralment oposats dels disc sí que son semblants a les nostres rectes euclidianes. Aquesta "distorsió" de les rectes pot ser interessant a l'aula perquè ajuda a visualitzar que estem en una geometria diferent a la del pla euclidià. No pensem que calgui entrar a l'aula en la justificació detallada d'aquesta deformació de les rectes, que prové de la projecció d'un hiperboloide en un pla. Tot i així, als comentaris d'aula finals us proposem una construcció en GeoGebra que pot il·lustrar aquesta conversió de rectes en arcs.

Rectes hiperbòliques en forma d'arc de circumferència (menys quan són un diàmetre del disc)

Però, tot i no entrar en argumentar el per què d'aquestes rectes, sí que pot ser convenient familiaritzar-se amb elles i veure que són úniques unint dos punts. Podem preparar una construcció en Geogebra com la següent, en la que veurem que hi ha infinits arcs de circumferència que uneixen dos punts, però només hi ha un sol cas en el que l'arc incideix ortogonalment en la circumferència del disc. A l'applet podem moure els punts A i B, però especialment el punt C que ens farà variar els arcs fins aconseguir el que talla amb 90º.

Enllaç a la construcció

Tenim redefinides les rectes. Els segments seran fragments, entre dos punts, d'aquestes rectes. Aquests segments son geodèsiques, ja que uneixen dos punts amb el trajecte més curt possible. Si un habitant d'aquest disc s'hi vol acostar a un altre, seguirà aquesta trajectòria visualment per a nosaltres, tot i que ell tindrà la sensació d'anar en línia recta.

Els angles es poden mesurar gairebé de forma euclidiana: serà el format per les tangents a les "rectes". Ara us recomanaríem obrir algun applet de GeoGebra que us permeti dibuixar rectes, mesurar angles, etc. Una molt bona possibilitat és aquest applet de Tibor Marcinek. També en teniu un altre amb el que hem fet l'animació de sota, Si proveu, veureu una cosa ben estranya: si el vèrtex de l'angle s'acosta al centre del disc l'angle és molt gran; si s'acosta a la vora es va reduint i tendint a zero.

GeoGebra de Soundmanbrad

El fet de que les nostres línies siguin el resultat de projeccions fa que no ens puguem refiar de la vista per comparar distàncies. Cal fer una observació important: segments de longituds visualment semblants tindran llargades diferents segons la zona del disc a la que estiguin; seran aparentment més "curts" a la zona central i més "llargs" a les vores del disc. De la mateixa forma, una mateixa distància "real" s'anirà reduint visualment a mesura que ens acostem a la vora del disc. Això implica que no podem comparar mai la longitud de dos segments a ull o, en general, ponderar llargades, ja que la seva aparença depèn de la posició al disc.

Aquest segment sempre mesura dues unitats

Si ja ens hem fet una idea de les noves regles de funcionament en quant a rectes, angles i distàncies podem fer, com a la proposta sobre la geometria esfèrica de l'article anterior, algunes tasques relacionades amb la comparació amb els postulats d'Euclides i a l'estudi dels triangles.

Mirem els postulats euclidians.

Si comparem els postulats euclidians, referits al pla, adaptats a les noves definicions del disc de Poincaré, observarem que els quatre primers són coincidents i que la discrepància la tenim en el cinquè, el de les paral·leles.

1r postulat. Per dos punts diferents només hi passa una recta.

2n postulat. Un segment rectilini pot ser allargat sempre.

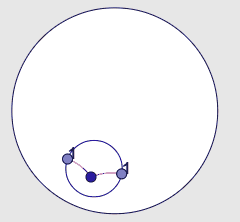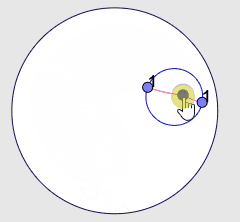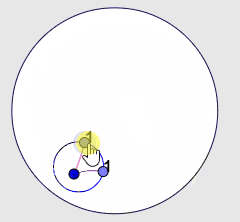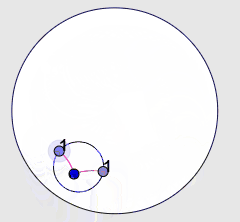3r. Postulat. Hi ha una sola circumferència amb un centre i un radi donats.

En aquest cas cal destacar que a la imatge tenim una circumferència que sempre té radi 1 però que queda visualment afectada pel canvi aparent de les distàncies. Fins i tot podem veure que el centre sembla progressivament més "excèntric" a mesura que ens acostem a la vora del disc.

4t postulat. Tots els angles rectes són iguals entre sí.

No em puc estar de comentar que aquest postulat sempre l'he trobat estrany. Especialment si tenim en compte que a la definició 10 del primer llibre trobem que "quan una línia recta que està sobre una altra fa que els angles adjacents siguin iguals, cadascun dels angles és recte, i la recta que està sobre l'altra es diu perpendicular a l'altra recta.".

I ara, finalment, bé la discrepància. Entenem com paral·leles rectes que no es tallen, com diu la definició 23 del llibre I dels Elements: "Rectes paral·leles són aquelles que, estant en un mateix pla i sent prolongades indefinidament en ambdós sentits, no troben una a una altra en cap d'ells.". El 5è postulat es pot formular dient que "Per un punt exterior a una recta només hi passa una paral·lela." Si practiquem amb alguns dels GeoGebra que hem proposat veurem infinitat de rectes externes a una recta donada que no la tallen mai: hi ha infinites paral·leles.

5è postulat: Per un punt a una recta passen infinites paral·leles.

Estudiem el triangle hiperbòlic.

Un triangle hiperbòlic és el que es forma amb tres geodèsiques d'una superfície hipèrbòlica. Com a l'esfera, les geodèsiques no tenen perquè coincidir amb els "paral·lels" que podem haver traçat a la superfície. Recordem, de pas, que les geodèsiques són els trajectes més curts entre dos punts sobre una superfície donada.

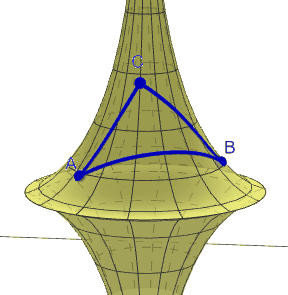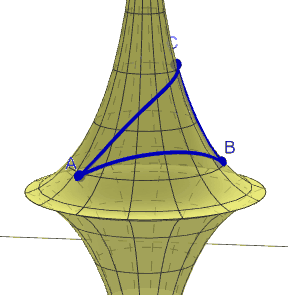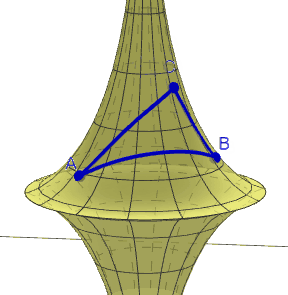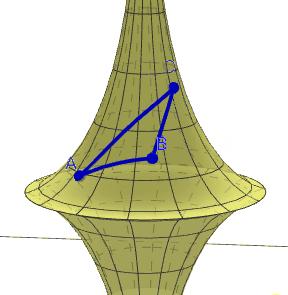Triangle sobre una pseuesfera. GeoGebra d'Humberto José Bortolossi

Anem ara a estudiar alguns aspectes relatius al triangle en el disc de Poincaré.

• Suma dels angles interiors

El millor és experimentar amb una construcció de GeoGebra com les que hem recomanat abans. El de Tibor Marcinek té una eina que mesura la suma dels angles directament. Podem començar amb els punts el més ajustats possible a l'exterior del disc i veure que la suma dels angles és pràcticament de 0º. Si els anem portant al centre del disc observarem que la suma s'acosta a 180º (π radians) sense arribar a aconseguir-los.

• Grandària dels triangles

Al pla euclidià els triangles poden ser infinitament grans. A l'esfera, de superfície limitada, no. I a la geometria hiperbòlica? Si hem fet l'experiment de l'apartat anterior haurem observat col·lateralment que la grandària està relacionada amb la suma dels angles (és a dir, dels tres angles concrets del triangle) i que, quan més grans son, més petita és la suma angular. Podem intuir que la grandària del triangle depèn proporcionalment dels seus angles i, de fet, com a la geometria el·líptica (la de l'esfera) dos triangles que tinguin els mateixos angles no son només semblants, com a l'euclidiana, sinó que son congruents, exactament iguals.

Si experimentem amb aquest applet de GeoGebra veurem que l'àrea (en un disc de radi 1) coincideix amb el defecte angular en radians: el que li falta per sumar els π radians dels triangles euclidians. En aquest cas, com vam comentar en l'exemple equivalent de la geometria esfèrica, és millor treballar amb radians perquè la relació es fa més evident.

Enllaç a la construcció

Tornem a la pregunta inicial: tenen una grandària il·limitada? La resposta és que no: la seva àrea no pot arribar a π unitats quadrades, quan el defecte angular és màxim: π radians.

Deixem una pregunta: com obtindrem el perímetre màxim?

• Rectes i punts notables del triangle

Gràcies a les aplicacions creades amb GeoGebra és relativament fàcil investigar aquest aspecte dels triangles hiperbòlics. Trobarem que, en general tot funciona com a la geometria euclidiana. Excepte una cosa: no tots els triangles tenen circumcentre i circumferència circumscrita. En determinades circumstàncies, que podeu investigar, el circumcentre surt fora del disc i no tenim circumferència circumscrita.

Enllaç a la construcció

Podeu investigar les altres rectes i punts en aquest altre GeoGebra creat per Szilassi Lajos. L'applet, per cert, pertany a un llibre molt complet sobre aquesta geometria.

• Teorema de Pitàgores

Si experimentem amb un applet com el proposat observarem que la suma dels quadrats dels catets és sempre inferior al quadrat de la hipotenusa.

Enllaç a la construcció

Construïm un quadrat

Pot ser un repte interessant a l'aula construir un quadrat. Entre altres coses perquè haurem de ressituar alguna idea. El quadrat ha de tenir els quatre costats i els quatre angles iguals. Pot ser interessant mirar si l'alumnat prioritza aquestes condicions o intenta imposar que els angles siguin de 90º. I, un cop decidit això, pensar com realitzar la construcció amb les eines disponibles.

I a l'aula?

• No recomanaríem treballar la geometria hiperbòlica sense haver fet abans l'esfèrica, que és més intuïtiva. Així com en el cas de la geometria esfèrica aconsellàvem molt el debat a partir de l'experimentació amb materials i recursos fets amb GeoGebra, aquí serà millor fer-ho només a partir d'aquests últims.
• Dels diferents models físics o plans per il·lustrar aquesta geometria optem pel Disc de Poincaré per la seva estranyesa en convertir les rectes en arcs de circumferència. Evidenciar aquesta estranyesa ens sembla una bona opció per diferenciar-la de l'euclidiana. Tot i que el model s'ha d'explicar i l'alumnat, en gran part, haurà de fer un "acte de fe" en aspectes com  les distàncies o les geodèsiques. Però la nostra intenció és introduir-nos en aquest món, no estudiar-lo amb profunditat ni fer justificacions plenes. Però si es vol il·lustrar una mica, també hi ha construccions en GeoGebra que ens hi poden ajudar. Per exemple, una en 3D d'Ayhan Aksoy.

Enllaç a la construcció

Sobre el model cal insistir, com hem comentat anteriorment, en el tipus concret d'arc que formen les rectes (ortogonals a la vora del disc) i que no es poden refiar de l'aparença visual per a valorar distàncies: una mateixa longitud es va empetitint visualment a mesura que s'allunya del centre del disc.

• Un cop entès-acceptat el model del disc de Poincaré sí que podem posar en debat, un a un, els postulats d'Euclides. Si volem, pel cas del cinquè, podem destacar que hi ha dues paral·lels límit (les que tallen la recta en el punt ideal de la vora del disc, que recordem no forma part del pla).  que s'anomenen hiperparal·leles, i altres paral·leles que no tallen la recta enlloc, i que s'anomenen ultraparal·leles.

• Hem recomanat l'estudi dels triangles i de la construcció del quadrat, però no cal dir que es poden investigar, experimentalment, o amb cerca documental, altres aspectes com l'adaptació exacta del teorema de Pitàgores o el valor de π.
• També es poden mirar altres adaptacions al pla de les les superfícies hiperbòliques com el model de Beltrami-Klein  (GeoGebra) o el semiplà superior de Poincaré (GeoGebra)
• Pot ser curiós cercar diferents exemples de mosaics hiperbòlics, a més del coneguts d'Escher.

• La matemàtica letona Daina Taimina ha fet i estudiat tot de superfícies hiperbòliques amb ganxet. Són ben boniques de veure i té moltes recollides al seu blog. Si voleu també podeu veure un Ted-talk en el què ho explica.

• I, com no, fer conèixer una mica la història d'aquesta geometria, especialment la dels seus creadors més importants: Nikolai Lobatxevski i János Bolyai