La situació és la següent: tenim un conjunt d'illes iguals de cases, posem-ne com les de l'Eixample de Barcelona. En la situació d'exemple tenim un rectangle de 4x7 illes. Si col·loquem un vigilant a una cruïlla només pot observar els carrers que s'hi troben a la cruïlla i el seu abast visual és de la longitud d'una illa, és a dir, fins a la cruïlla següent (a l'Eixample serien 100 m). Quin és el nombre mínim de vigilants que calen per controlar tots els carrers?
Pots practicar amb aquest applet enllaçat clicant sobre els botons que hi ha a les cruïlles.
 |
| Enllaç a l'applet (flash) |
Si observes la solució mínima (que imaginem que hauràs obtingut sense dificultats especials o, si més no després de no masses proves) veuràs que la distribució dels vigilants segueix un patró força regular. La investigació que proposem és justament aquesta: es pot saber la quantitat mínima de vigilants, sense distribuir-los, coneixent quantes illes té cada costat del rectangle.
T'animes a investigar?
Aquest tipus de problemes es poden atacar de formes diverses i, segon l'edat amb que treballem, a més, graduarem més o menys el repte.
Una de les opcions de treball és reduir casos i fer taules que recullin les dades. Si ens interessa, fins i tot podem dividir les taules en columnes que separin la quantitat de vigilants que vigilen dos carrers (els de les cantonades), dels que en vigilen tres (els de les vores) i dels que n'observen quatre (els dels carrers interiors).
T'animes a investigar?
Aquest tipus de problemes es poden atacar de formes diverses i, segon l'edat amb que treballem, a més, graduarem més o menys el repte.
Una de les opcions de treball és reduir casos i fer taules que recullin les dades. Si ens interessa, fins i tot podem dividir les taules en columnes que separin la quantitat de vigilants que vigilen dos carrers (els de les cantonades), dels que en vigilen tres (els de les vores) i dels que n'observen quatre (els dels carrers interiors).
Analitzar organitzadament
Mirem un exemple: en aquest gràfic mostrem la informació per casos de tres illes en horitzontal. A cada cas indiquem:
- la mida de la graella d'illes
- els vigilants de 2, 3 i 4 carrers (per aquest ordre)
- el total de vigilants
Convé tenir clar que en cada cas tenim la quantitat mínima de vigilants.
 |
| Exemple d'optimització en 2x2 |
Aquest estudi de graelles es pot repartir entre diferents grups de la classe i després recollir i contrastar dades. Podrem reunir taules com les següents.
| Graella |
Vigilants
|
Graella |
Vigilants
|
Graella |
Vigilants
|
|||||||||||
| 2 | 3 | 4 | total | 2 | 3 | 4 | total | 2 | 3 | 4 | total | |||||
| 1x1 | 2 | 0 | 0 | 2 | 2x1 | 2 | 1 | 0 | 3 | 3x1 | 2 | 2 | 0 | 4 | ||
| 1x2 | 2 | 1 | 0 | 3 | 2x2 | 0 | 4 | 0 | 4 | 3x2 | 2 | 3 | 1 | 6 | ||
| 1x3 | 2 | 2 | 0 | 4 | 2x3 | 2 | 3 | 1 | 6 | 3x3 | 2 | 4 | 2 | 8 | ||
| 1x4 | 2 | 3 | 0 | 5 | 2x4 | 0 | 6 | 1 | 7 | 3x4 | 2 | 5 | 3 | 10 | ||
| 1x5 | 2 | 4 | 0 | 6 | 2x5 | 2 | 5 | 2 | 9 | 3x5 | 2 | 6 | 4 | 12 | ||
| 1x6 | 2 | 5 | 0 | 7 | 2x6 | 0 | 8 | 2 | 10 | 3x6 | 2 | 7 | 5 | 14 | ||
| 1x7 | 2 | 6 | 0 | 8 | 2x7 | 2 | 7 | 3 | 12 | 3x7 | 2 | 8 | 6 | 16 | ||
| 1x8 | 2 | 7 | 0 | 9 | 2x8 | 0 | 10 | 3 | 13 | 3x8 | 2 | 9 | 7 | 18 | ||
| 1x9 | 2 | 8 | 0 | 10 | 2x9 | 2 | 9 | 4 | 15 | 3x9 | 2 | 10 | 8 | 20 | ||
| 1x10 | 2 | 9 | 0 | 11 | 2x10 | 0 | 12 | 4 | 16 | 3x10 | 2 | 11 | 9 | 22 | ||
| Graella |
Vigilants
|
Graella |
Vigilants
|
Graella |
Vigilants
|
|||||||||||
| 2 | 3 | 4 | total | 2 | 3 | 4 | total | 2 | 3 | 4 | total | |||||
| 4x1 | 2 | 3 | 0 | 5 | 5x1 | 2 | 4 | 0 | 6 | 6x1 | 2 | 5 | 0 | 7 | ||
| 4x2 | 0 | 6 | 1 | 7 | 5x2 | 2 | 5 | 2 | 9 | 6x2 | 0 | 8 | 2 | 10 | ||
| 4x3 | 2 | 5 | 3 | 10 | 5x3 | 2 | 6 | 4 | 12 | 6x3 | 2 | 7 | 5 | 14 | ||
| 4x4 | 0 | 8 | 4 | 12 | 5x4 | 2 | 7 | 6 | 15 | 6x4 | 0 | 10 | 7 | 17 | ||
| 4x5 | 2 | 7 | 6 | 15 | 5x5 | 2 | 8 | 8 | 18 | 6x5 | 2 | 9 | 10 | 21 | ||
| 4x6 | 0 | 10 | 7 | 17 | 5x6 | 2 | 9 | 10 | 21 | 6x6 | 0 | 12 | 12 | 24 | ||
| 4x7 | 2 | 9 | 9 | 20 | 5x7 | 2 | 10 | 12 | 24 | 6x7 | 2 | 11 | 15 | 28 | ||
| 4x8 | 0 | 12 | 10 | 22 | 5x8 | 2 | 11 | 14 | 27 | 6x8 | 0 | 14 | 17 | 31 | ||
| 4x9 | 2 | 11 | 12 | 25 | 5x9 | 2 | 12 | 16 | 30 | 6x9 | 2 | 13 | 20 | 35 | ||
| 4x10 | 0 | 14 | 13 | 27 | 5x10 | 2 | 13 | 18 | 33 | 6x10 | 0 | 16 | 22 | 38 | ||
No són taules de tot senzilles inicialment. Les taules "senars" d'una, tres i cinc fileres són més regulars. Però les "parells", de dues, quatre i sis fileres, tenen com una doble regularitat, la de columnes senars i la de columnes parells. En tot cas és interessant descobrir les pautes, intentar fer conjectures de casos, observant la taula, i comprovant després amb el dibuix.
També, tot fent la taula, podem aprofitar observant la commutabilitat. Per exemple, una graella de 3x4 és idèntica a una de 4x3.
Cap a una fórmula general
Sense passar per les taules (o bé venint d'elles) podem anar cap la descoberta d'una fórmula general a partir de les regularitats del dibuix. Amb alumnat d'ESO por ser més eficient, encara que també ens podríem arriscar a provar-ho al final de la primària.
Mirem una altra vegada el dibuix de graelles d'illes de tres fileres:
Els "dos" vigilants de cada columna es corresponen amb la meitat dels carrers horitzontals (en tenim 4 i col·loquem un vigilant cada dos). Com que a cada carrer vertical en posem dos, i en tenim 6 de carrers verticals, el total vindrà de multiplicar 2x6 = 12.
En general,
- si diem a a les illes en horitzontal tindrem a+1 carrers i haurem de posar (a+1)/2 vigilants a cada carrer vertical.
- si diem b a les illes en columna tindrem b+1 carrers verticals.
- per tant la fórmula per calcular el total de vigilants serà:
Hi ha una altra forma d'arribar-hi potser més planera. Es basa en dues idees:
- Hem de comptar les cruïlles (a+1)·(b+1)
- La solució mínima passa per cobrir-ne la meitat d'aquestes cruïlles.
Però aquesta fórmula, si ens hi fixem, no funciona sempre. Per exemple en el cas següent 4x6, on la previsió diria 17,5 i, en realitat, tenim 17.
Illes "parells"
No és difícil veure els casos en què falla la fórmula ni com corregir-la.
- Falla quan a i b són parells.
- Només cal restar 0,5 al resultat
Haig de reconèixer haver fet trampa anteriorment triant un cas de fileres senar per persentar el problema. La fórmula i l'explicació servirien igualment per a un nombre parell de fileres i senar de columnes. Només cal girar 90º la graella d'illes.
Podem aplicar el raonament que hem fet abans estudiant la quantitat de cruïlles i considerant que l'optimització serà omplint la meitat de vigilants. En el cas de que els carrers verticals siguin senars a la darrera columna ens podem estalviar un vigilant a una de les cruïlles. L'alternança 2-3-2-3... acaba en 2
La fórmula que ens donarà el mínim de vigilants serà:
Hi altres fórmules equivalents segons com enfoquem el recompte de vigilants (i a classe els nois i noies ho fan de formes molt diferents).
- podem imaginar els vigilants formant un rectangle i afegir la quantitat que "tenim de més" a la darrera fila.
- podem observar parelles de carrers consecutius. En el cas de 4x6 podem observar que tenim tres parelles (la meitat de 6) amb 5 vigilants (4+1) i que hem d'afegir al final dos vigilants (4/2).
- podem imaginar que tenim un carrer menys, aplicar la fórmula dels senars, i afegir els vigilants de la darrera fila o columna que no hàgim tingut en compte.
- de forma similar, podem imaginar que tenim un carrer més i compensar eliminant els del carrer sobrer.
- si a un nombre senar com 13 anomenem "meitat gran" a 7 i "meitat petita" a 6 podem veure que (i perdoneu la redacció embarbussada) a la meitat gran dels carrers verticals tenim una quantitat de vigilants igual a la meitat petita de carrers horitzontals i a la meitat petita de carrers verticals tenim una quantitat de vigilants igual a la meitat gran de carrers horitzontals. Aquesta observació ens permet transcriure una altra fórmula.
Les coses bones d'aquest problema per a l'aula
En el fons el que faré és una llista de les coses que més m'agraden d'aquest problema:
- és un problema que treballa amb dues variables (illes en vertical i en horitzontal) però produeix un patró clar. Sovint treballem només amb un sola variable.
- el patró presenta una petita irregularitat en el cas que els dos nombres són parells. Aquesta petita irregularitat en comptes de complicar el problema l'enriqueix.
- és un patró que té molt de geomètric i és fàcilment visualitzable.
- parteix d'un problema de visualització que ja té el seu "què" propi. El "què" d'optimització i generalització se'n deriva.
- és abordable a diferents edats segons com el plantegem, què demanem i què esperem. Amb els més petits ens podem conformar en el descobriment de les regularitats a les taules (senzilles o complexes). En alguns casos podem demanar com calcular alguna de les regles però sense necessitat d'arribar a escriure una fórmula: explicant-lo de forma retòrica.
- segons la visualització que es faci de la distribució s'obtenen formes de càlcul diferents. Per tant, permet formes diverses d'abordatge i es facilita que tothom pugui trobar "la seva solució". Amb els més grans es poden manipular les diferents expressions algebraiques per veure la seva equivalència.













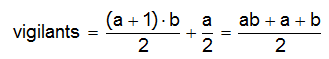



Cap comentari:
Publica un comentari a l'entrada