Hi ha problemes de recreació matemàtica que són molt més antics del que ens pensem. Un d'ells és el clàssic problema del pastor, la col, la cabra i el llop. Aquest problema apareix escrit, per primera vegada, al llibre del segle IX d'Alcuí de York Propositiones ad acuendos iuvenes (Problemes per afinar l’enginy dels joves). És el 18è problema del text i el seu enunciat original era aquest:
“Un home havia de portar a l'altra banda del riu un llop, una cabra i una col, però no va trobar cap altre vaixell que un que només podia portar-ne dos d'ells. I va ser dit, que totes aquestes coses arribaren a l'altra banda il·leses. Digui, qui pugui, com els van poder traslladar il·lesos a l'altre costat”
“Hi havia tres homes, cadascun amb una germana soltera, que havien de creuar un riu. Cada home desitjava la germana del seu amic. Arribant al riu, només van trobar una petita barca en què podien creuar dues persones cada vegada. Digui, qui pugui: Com van creuar el riu, de manera que cap de les germanes fos maculada pels homes?”
Dit més planer: les germanes podien estar soles amb les altres germanes, però si hi havia homes presents, un d'ells havia de ser el seu germà. En general, pel context narratiu de versions posteriors, se'l coneix com el problema dels "marits gelosos". El problema apareix a llibres ben clàssics: als Annales Stadenses d'Alberto di Stade (sobre el 1250), al De viribus quantitatis (Del poder dels nombres) de Luca Pacioli i al Libro dicto giuochi matematici de Pietro di Nicolao da Filicaia (tots dos manuscrits fets sobre el 1500), i que ja comencen a parlar de la generalització del problema. També el trobem al General tratatto (1556) de Niccoló Tartaglia, que dona una solució errònia pel cas de quatre parelles, o als Problèmes plaisants et délectables qui se font par des nombres (1612) de Claude-Gaspar Bachet, que també aborda el cas general. La solució general completa la trobem al primer volum de les Récréations mathématiques (1891) d'Édouard Lucas.
En primer lloc, us animem a agafar unes cartes de la baralla i solucionar el problema.
- En els viatges d'anada descartem, sempre que sigui possible, que només viatgi una persona, perquè hauria de retornar ella mateixa amb la barca i seria un moviment infructuós.
- Dos homes no poden marxar perquè quedarien dues dones sense el seu marit.
- Només hi ha dos moviments possibles; que passi un matrimoni o dues dones. Provem la primera opció: passa un matrimoni. (Ja apuntem que els dos moviments porten a situacions equivalents ràpidament).
- En els viatges de tornada prioritzarem que només torni una persona, perquè l'objectiu és deixar a l'altra riba el màxim de gent. Així i tot, si en algun moment és absolutament necessari, contemplarem la possibilitat que en tornin dues.
- La dona no pot tornar perquè a l'altra riba estaria sense el seu marit. Per tant, tornar l'home.
- Si marxa una altra parella la dona blava estarà acompanyada d'un altre home que no és el seu marit. Descartem aquest moviment.
- També descartem que passin dos homes, perquè l'altre quedaria amb una dona que no és la seva.
- Per tant, passen les dues dones.
- La parella blava no pot passar perquè l'home estaria a l'altra riba amb les altres dones sense els seus marits.
- Una parella home-dona que no són parella també incompliria les normes.
- L'única possibilitat és que passin els homes que tenen les parelles a l'altra banda.
- Un home sol no pot tornar perquè deixaria la seva parella amb l'altre.
- Una dona sola o les dues no poden tornar perquè a l'altra riba estarien amb un home que no és el seu marit.
- Que tornin els dos homes seria tornar a la situació anterior.
- Només hi ha una opció: que torni una parella.
- Que passi una parella seria retrocedir a la situació anterior.
- Les dues donen no poden passar perquè estarien a l'altra riba amb un home i sense els seus marits.
- Només queda que passin els dos homes.
- No té sentit que tornin els dos homes que acaben d'arribar.
- L'altre home no pot deixar la dona.
- Ha de tornar, forçosament la dona.
- Una sola opció: passen dues dones.
- Cap dels homes que no sigui la parella de la dona que ha quedat pot tornar. La seva parella sí.
- També pot tornar una de les dones. Agafem aquesta opció (l'altra també soluciona el problema).
- Passen les dues dones i el problema està resolt.
"I si hi havia 4 homes i quatre dones, envieu primer 2 dones i feu que una d'elles vingui a agafar-ne una altra, i traieu-la d'allà, una d'elles ve d'aquí amb la barca i s'emporta la quarta dona, (...), una d'elles ve d'aquí amb la barca, i s'acosta al seu marit, aleshores s'aixequen dos homes, i entren a la barca, i se'n van al costat de les seves dames, aleshores aquella dama que és la que no va acompanyada l'entra a la barca, i ve a endur-se el seu marit, i se'l porta d'allà..."
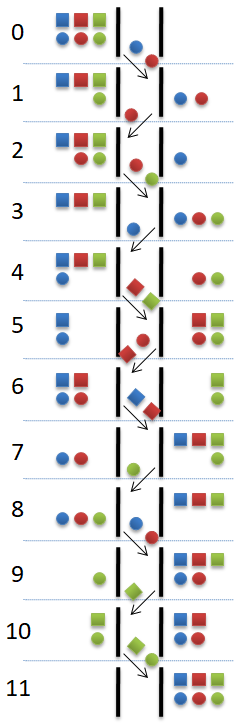
Si representem la solució completa veurem que després del setè moviment a la riba dreta hi ha més dones que homes, cosa que contravé les normes del problema. Amb un esquema de la resolució descrita ho veurem més clar.
- En general, a la segona riba, hi haurà cada vegada, després de dos viatges, una persona més.
- Hi haurà un moment que a la segona riba hi haurà cinc persones. Només hi ha quatre combinacions possibles d'homes i dones: 4 i 1, 3 i 2, 2 i 3,1 i 4.
- No poden ser les dues primeres (quatre dones i un home o tres dones i dos homes) perquè s'incomplirien les regles del problema.
- No pot ser la tercera, dues dones i tres homes, perquè a l'altra riba hi hauria dues dones i un home, que tampoc compleix les normes.
- La quarta, una dona i quatre homes, sembla possible. A l'altra riba tindríem tres dones soles. Estudiem com es pot haver arribat a aquesta situació:
- Si de la primera riba han vingut dos homes abans hi havia dues dones i tres homes. Impossible.
- Si han vingut un home i una dona, abans hi havia un home i quatre dones. Impossible també.
"Llavors tu pots amb el teu enginy fer-ho amb 4 marits i 4 dones, i amb 5, i amb 6, etc. Però tingueu en compte que es necessita que la barca tingui capacitat per un menys que la quantitat de parelles que siguin, perquè si són 4 marits i tantes dones, cal que a la barca càpiguen 3 persones, i si fossin 5 cal que la barca tingui capacitat per a 4 i així fins a l'infinit, i si no treballaràs en va".
Aquesta observació no és del tot correcta per dues raons. La primera és que, com assenyalava Luca Pacioli al De viribus quantitatis, el cas de cinc parelles es pot resoldre amb una barca per a tres persones. Us convidem a provar-ho.
La segona raó és que, a partir de 6 parelles, la cosa varia. Avancem en el temps fins al capítol que Lucas dedica a aquest problema a les seves Récréations mathématiques: "El joc de les travessies en barca".
"Una companyia d'infanteria va arribar fins a la riba d'un riu, però el pont estava trencat i el riu era profund. El capità es va adonar que, a prop de la riba, dos nens jugaven a un petit bot; la barca era tan petita que només podia portar un soldat [o un nen]. Què va fer el capità perquè tots els soldats de la seva companya passessin el riu?"
No és un problema especialment complicat:
- passen els dos nens i un torna.
- passa un soldat i torna el nen que havia quedat.
- tornen a passar els dos nens i un torna.
- passa un altre soldat i torna el nen que estava a l'altra riba.
- passen els dos nens...
El problema encara seria més fàcil si a la barca hi caben dues persones. No caldrien ni els nens:
- passen dos soldats i torna un.
- passen dos soldats i torna un
- etc.
- passen dues parelles i una torna.
- passen dues parelles i una torna
- etc.
A l'apèndix del llibre Lucas ens posa el marc general del problema.
| Parelles | Capacitat barca | Viatges |
| 2 | 2 | 5 |
| 3 | 2 | 11 |
| 4 | 3 | 9 |
| 5 | 3 | 11 |
| Més de 5 | 4 | 2n-1 |
- Posem una illa al riu
- No tothom sap remar
- Majories
"Tenim en un costat del riu tres missioners i tres zombis que volen passar a l'altra riba amb un bot on només hi caben dues persones. Per evitar que els zombis es mengin els missioners, mai hi pot haver més zombis que missioners a cap de les ribes. Si estàs pensant que per què no matar els zombis i solucionar el problema amb tres viatges, la resposta és que els missioners, pels vots promesos, no poden matar… ningú. La pregunta ara és: quin és el mínim nombre de viatges necessari perquè les sis… ehem… “persones” passin a l'altra riba i en quin ordre ho han de fer?
- Tornem a Alcuí de York
"Un home i la seva dona, cadascun del pes d'un carro carregat, van tenir dos fills cadascun del pes de mig carro. Necessitaven creuar un riu però la barca que tenien només podia suportar el pes d'un carro. Qui sigui capaç, que faci el transport perquè el vaixell no s'enfonsi."
- Henry Dudeney
"Fa molts anys, en temps del contrabandista conegut com "Rob Roy of the West", una banda pirata va enterrar a la costa de South Devon uns tresors que, per descomptat, van deixar abandonats de la manera habitual inexplicable. Temps després el seu parador va ser descobert per tres pagesos, que van visitar el lloc una nit i es van repartir el botí. Giles va agafar tresors per valor de 800 lliures, Jasper per valor de 500 lliures, i Timothy pel de 300 lliures. Van haver de creuar el riu Axe en un lloc on havien deixat una barca preparada. Aquí, però, van trobar una dificultat que no havien previst. La barca només podia portar dos homes, o un home i un sac, i tenien tan poca confiança, l'un en l'altre, que ningú no podia quedar sol a terra o a la barca amb més de la seva part del botí, encara que dues persones (que es podien vigilar entre ells) podien quedar-se amb més del que els corresponia. El trencaclosques consisteix a mostrar com van travessar el riu en el menor nombre de travessies possibles, emportant-se els seus tresors. No es poden utilitzar trucs, com cordes, "ponts volants", corrents, natació o tripijocs similars."
- No entrarem ara en reivindicar amb profunditat el paper educatiu de les recreacions matemàtiques. Algun dia ens hi posarem. Ara només volem recordar que són reptes que mobilitzen i que, sovint, no demanen coneixements matemàtics especials.
- Si és possible, aquests problemes és convenient treballar-los manipulativament. Els materials no són complicats. El de les tres parelles ja hem recomanat fer-lo amb cartes de la baralla. Però també es pot anar una mica més enllà. Treballar-los com un rol-play: amb alumnes representant cada paper. I es poden fer vídeos!
- És evident que els contextos dels problemes són més que discutibles. Es pot valorar si presentar-los tal qual. En aquest cas, caldria esmentar el moment històric i, segurament, discutir, en un altre moment o en un altre espai, les qüestions que actualment no es consideren acceptables. També es poden canviar els contextos de presentació. Hi ha una versió russa antiga del problema del marits gelosos en un context que són tres pares i tres fills i els fills no volen quedar-se sols sense el seu pare. Els contexts fantàstics també donen joc. Us animem a compartir-los com a comentaris.
- Els problemes són abastables a diferents nivells educatius. Es poden treballar els problemes principals i anar proposant variants després, distribuint-les segons el grau de dificultat.
- Sempre és interessant veure alguna demostració. La de la impossibilitat de fer el problema amb quatre parelles i una barca de dues places es pot guiar: fer observar les quatre situacions possibles amb cinc persones a la segona riba i fer-les analitzar.
- Ens sembla interessant, per no dir important, fer una mica de viatge històric pels problemes.
- Relacionats amb el problema del pastor, la col, l'ovella i el llop, ens agradaria comentar un parell de llibres. Per als més menuts hi ha un magnífic llibre il·lustrat de Philippe Corentin: L'ogre, el llop, la nena i el pastís, que va plantejant les situacions amb mitges pàgines superposables. Per alumnat més gran hi ha un irònic conte d'Allan Ahlberg: El chico, el lobo, la oveja y la lechuga... Un enigma por resolver, que fa una mena de reportatge periodístic de com s'hi van trobar els protagonistes en tan fantàstica situació i com la van resoldre.
- I si voleu una versió divertida del problema més clàssic aquí yeniu un del dibuixant Tom Gauld extreta del seu llibre de tires còmiques sobre ciència "El departamento de las teorías alucinantes"


















.jpg)




.jpg)
Cap comentari:
Publica un comentari a l'entrada