El nim del doble (2)

 A l'article anterior a aquest (El Nim "del doble" - 1) presentàvem i iniciàvem l'anàlisi d'un joc d'estratègia per a dos jugadors de tipus Nim. En aquest cas, les regles són les següents: hi ha una pila de fitxes de la que cada jugador pot agafar tantes fitxes com vulgui entre una i el doble de les que hagi agafat el jugador anterior. Qui deixa la taula neta guanya. I, a la jugada inicial es poden agafar totes les fitxes que es vulguin menys una.

Exemple de partida amb 10 fitxes inicials.
La partida es llegeix d'esquerra a dreta i guanya verd

Vam fer tots de diagrames en arbre per estudiar diferents quantitats de fitxes inicials i de conjectures equivocades. Cap al final de l'article vam veure que hi apareixien misteriosament els nombres de Fibonacci. Si la quantitat de fitxes inicial és un nombre de Fibonacci sembla que hi ha estratègia per al 2n jugador. Si no ho és el primer pot guanyar si deixa al contrari amb una quantitat de fitxes que sigui un nombre de Fibonacci. Però també vam veure que això no ho podem fer sempre sempre. Posàvem l'exemple de jugar amb 12 fitxes. Si A (el 1r jugador) agafa 4 deixa a B (el 2n jugador) amb 8, que és un nombre de Fibonacci, perdrà perquè B, que pot agafar fins al doble de la jugada anterior, pot agafar les 8 que queden i guanyar. Després vam fer l'arbre d'estudi del joc per a 12 fitxes i vam veure que la sortida guanyadora era 1 (11), que entenem com "agafar-ne una i deixar-ne 11".

Estratègia per a A per a 12 fitxes

Deixar 11 fitxes no és "deixar un nombre de Fibonacci". Per tant vam concloure que havíem d'estudiar més el problema. I és el que farem ara.

T'animes a seguir llegint?

La crisi es fa més gran

La primera pregunta que em vaig fer, en la situació explicada, era que què tenia el 12 d'especial. Hi havia una resposta immediata: és un nombre que és una vegada i mitja més gran que un nombre de Fibonacci i que és múltiple de tres. Si fem alguns càlculs veurem que si multipliquem qualsevol nombre de Fibonacci parell per 1,5 obtindrem un múltiple de tres (de fet no cal que sigui de Fibonacci perquè passi això).

A primer cop d'ull sembla que seran poques les partides que ens donin problemes. Per a 3 i 12 fitxes ho tenim resolt i per a 51, 216, etc... no. És feixuc fer tants arbres de joc tan grans. Però continuant investigant, ens trobem amb un altre cas problemàtic i que és diferent de l'anterior: 20 fitxes inicials. Segons la nostra conjectura la jugada d'A seria deixar 13 fitxes. Però per fer-ho n'ha d'agafar 7. Si B pot jugar "fins al doble" de 7 (14) pot agafar totes les que queden i A perdrà. Per tant amb 20 no podem "atacar" directament un nombre de Fibonacci. La crisi és més gran del que pensàvem! Hi ha més nombres problemàtics!

Mirem-ho amb detall. Com són els "nombres problemàtics" per a iniciar una partida? Són aquells que estan a una distància prou gran  del nombre de Fibonacci menor com perquè el doble d'aquesta distància sigui igual o més gran que aquest nombre de Fibonacci. La meitat d'aquest nombre ens marcarà una frontera. Mirem-ho amb 20. El nombre de Fibonacci menor és 13 (i la seva meitat 6,5). La distància és 7 és més gran que 6,5. Per tant, si afagem 7, que té com a doble 14, el rival podrà agafar tot el que quedi. Si ho mirem amb 32 fitxes inicials el nombre de Fibonacci a assolir és 21, que està a una distància d'11. El doble és 22, superior a les 21 fitxes que queden. En general, si anomenem Q a la quantitat inicial i F_n al nombre de Fibonacci immediatament menor que Q, podem expressar matemàticament així el "nombres problemàtics!:

I podem fer una llista de nombres problemàtics: 

12 | 20 | 32, 33 | 51, 52, 53, 54 | 83, 84, 85, 86. 87, 88 | etc.

A l'article anterior havíem vist l'arbre de joc de 12. La primera jugada havia de ser 1.

Mirem l'arbre per a 20 fitxes inicials. Veurem que la jugada inicial a des ser agafar-ne 2. Si escrivim la jugada com a 2(18) descobrirem altres jugades intermèdies guanyadores i que assenyalem amb el costat del requadre marcat en vermell. Un parell d'aquestes, com 1(13) i 2(13), es reutilitzen en el mateix arbre.

Quina serà la jugada inicial per al següent, és a dir, per a 32? Fen l'arbre de l'estratègia per a 32, l'arbre de decisions:

Descobrim tres jugades intermèdies guanyadores a més de la inicial: 1(24), 1(26) i 2(26)

La jugada inicial és 3. A més descobrim altres situacions intermèdies guanyadores: 3(39), 2(26) i 1(26)

Tenim per a 12 una sortida d'1, per a 20, una sortida 2, per a 32 una sortida 3. I per a 33, el següent nombre problemàtic? Serà 4? O serà 5, el següent nombre de Fibonacci? Doncs ni un ni l'altre: és 1. Mirem l'arbre:

Descobrim tres jugades noves guanyadores: 1(32), 1(29) i 2 (29)

Fem resum del que tenim

Potser és hora de fer una llista del que sabem i del que no:

Sabem	No sabem
Si Q inicial és un nombre de Fibonacci,     l'estratègia guanyadora és per a B.	No tenim cap demostració de que això sigui sempre cert. Tampoc disposem d'un mètode general per a saber quina jugada hem de fer de resposta a A. Només sabem respondre en alguns casos.
Si Q inicial no és un nombre de Fibonacci, l'estratègia guanyadora és per a A.	No tenim cap demostració de que això sigui sempre cert. Tampoc disposem d'un mètode general per a saber quina jugada hem de fer de resposta a B, excepte en alguns casos.
Davant de cada situació de joc, el primer que hem de mirar és si podem agafar totes les fitxes. Si és així guanyem directament.
Si no podem agafar totes les fitxes la jugada guanyadora és deixar al contrari el nombre de Fibonacci immediatament posterior a la quantitat de fitxes total, però només si la jugada que fem és inferior a la meitat de fitxes que deixem, és a dir, a la meitat d'aquest nombre de Fibonacci. De no ser així regalem la victòria al contrari.	No tenim molt clara la raó de fons de per què els nombres de Fibonacci són "guanyadors". Aquesta idea es basa només en l'observació de que si Q (inicial o d'un moment de la partida) és un nombre de Fibonacci és perdedor per al jugador que faci la primera jugada.
Tenim "nombres problemàtics" que no ens deixen aplicar les jugades anteriors. Són de la forma	Quan Q és un "nombre problemàtic", com 12, 20, 32, etc. no tenim un mètode general per a saber la jugada que hem de fer. Només hem pogut observar que acostumen a ser jugades agafant poca quantitat de fitxes: 1, 2, 3... Poden ser nombres naturals qualsevol o nombres de Fibonacci. No hem arribat més lluny per saber-ho.
Tenim una llista de jugades guanyadores clares. Hi ha jugades "fibonaccianes" com 1(3) |1(5) i 2(5) | 1(8), 2(8) i 3(8) | etc. Aquestes tenen un patró que ja hem descrit abans. Però hi ha jugades "no fibonaccianes" que ens poden ser d'utilitat durant el desenvolupament de la partida. De moment tenim aquestes: 1(11), 1(16), 1(18), 2(18), 1(26), 2(26), 1(29), 2(29), 3(39), 1(32).	No sabem el patró de les jugades "no fibonaccianes". Ens les trobem durant l'anàlisi del desenvolupament d'una partida quan no podem agafar tot el que queda directament o no podem accedir directament a un nombre de Fibonacci sense deixar que el contrari, a continuació, pugui emportar-se tot el que queda.

Com veiem podem guanyar moltes partides, tenim molts arbres fets i jugades intermèdies que ens orienten, però tenim llacunes grans i tampoc hem descobert el patró general de l'estratègia... si existeix.

Un parèntesis "Fontià"

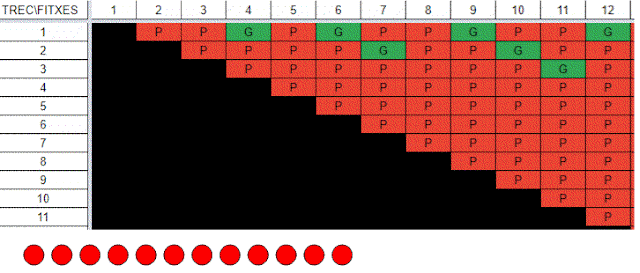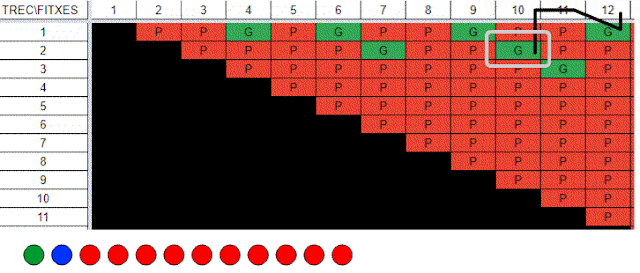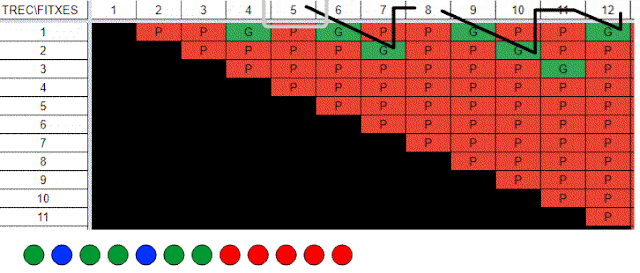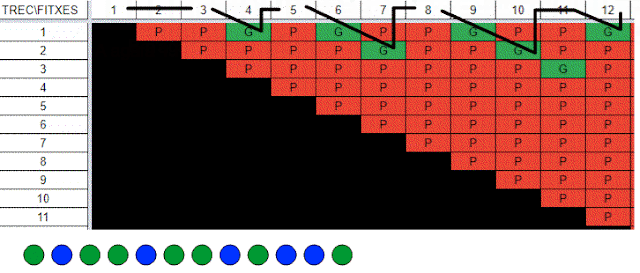
Una hora després de publicar la primera part d'aquests articles dedicats al joc del "nim del doble" vaig rebre un document d'en Jordi Font. Era el seu anàlisi del joc. Més brillant i concís que totes les tirallongues que us he anat clavant. És un full de càlcul de 89 columnes i 88 files. Cada columna és la quantitat Q que ens podem trobar durant una partida des de l'inici. I cada fila representa la quantitat de fitxes que podem treure. Cada cel·la ens indica com és una situació de joc. Així cada casella indicala quantitat de fitxes que hi ha i què passa segons les que agafem agafem: si és una jugada guanyadora (verd) o si és perdedoraperdedora (vermell).

Amb 9 fitxes, si agafem 4, perdrem. Amb 11 si n'agafem 3 guanyarem

La taula és una mena de mapa per a realitzar una partida, Veiem un exemple de com resseguir el mapa amn partida que comença amb 12 fitxes.

Però la taula d'en Jordi Font té una altra virtut. Si li fem una ullada podem intuir una certa regularitat en les posicions de les jugades guanyadores. Observeu les línies verdes.

Tot i així "una certa regularitat" no significa "una norma clara". Tenim més informació per anar jugant, però no tenim encara definida una norma general. Podeu veure la taula d'en Jordi amb més detall si obriu aquest document en pdf. També cal dir que al seu document fa taules semblants si el límit de la jugada màxima és el triple i el quàdruple. I que ja té anotades altres variants per a estudiar com que les quantitats de fitxes a treure siguin nombres primers. Aquest home és imparable.

I ara reprendrem el nostre estudi general del joc.

Demanem ajuda... i la trobem

L'ideal en l'estudi de jocs és treballar en equip. S'amplien les visions. Però, al no disposar d'equip, el que he fet és demanar ajuda a Google posant com a cerca una pista que tenim. I cerquem "nim fibonacci".

Un dels enllaços que he trobat és un simulador per a jugar en línia. Ha estat creat per Andy Long i pot ser molt útil per practicar amb un "jugador expert". Una de les coses que permet és triar la quantitat de fitxes de l'inici. I sempre seràs el primer jugador.

https://ja.cat/o9zr6

Un altre és la Viquipèdia. En el seu article en castellà només explica el joc. Però en la versió anglesa sí que trobem l'estratègia general explicada. Però, abans de compartir-la, avanço que dubto que l'hagués descobert. Entre altres coses perquè fa servir un teorema sobre els nombres de Fibonacci que desconeixia.

Teorema de Zeckendorf:  tot enter positiu es pot representar, de forma única, com la suma d'un o més nombres de Fibonacci diferents, de manera que la suma no inclogui dos nombres de Fibonacci consecutius.

Veiem exemples:

• 12 = 8+3+1
• 19 = 13+5+1
• 32 = 21+8+3
• 347 = 233+89+21+3+1

Si voleu podeu trobar una "calculadora" de descomposicions de Zeckendorf en aquest enllaç del web dCode.xyz.

A la mateixa Viquipèdia trobem una bonica representació gràfica de les primeres descomposicions.

L'estratègia descrita és la següent: a cada situació de joc fem la descomposició de Zeckendorf de la quantitat de fitxes del tauler. La tirada que hem de fer és el nombre més petit de Fibonacci de la descomposició. Amb un parell d'observacions:

• Si tenim una tirada directa per agafar totes les fitxes, l'hem de fer.
• Si la quantitat trobada és un nombre de Fibonacci (això només hauria de passar a la situació inicial) estem en una situació perdedora. Només ens queda anar jugant aleatòriament i esperar que l'altre jugador s'equivoqui.

Mirem un exemple de partida que comença amb 48 fitxes. Observarem que B, encara que intenti aplicar sempre la mateixa estratègia , no podrà fer mai la seva "jugada guanyadora" i haurà d'anar jugant "a l'atzar".

I a l'aula?

Evidentment, si no s'han treballat mai jocs d'estratègia i el que volem és trobar el mètode guanyador, s'ha de començar per un Nim normal. Per exemple, començar amb 21 fitxes i podent-ne agafar 1, 2 o 3 a cada jugada. És un joc que està perfectament a l'abast des de l'educació primària. Fins i tot amb els més petits es pot simplificar amb menys fitxes, posem-ne 13, i agafant-ne 1 o 2. Si només volem jugar, sense aprofundir massa, el nim "del doble" té unes regles prou senzilles per jugar-se a qualsevol edat. I amb els més petits pot ser una bona pràctica de dobles, donat que, cada vegada, hem de saber fins a quantes fitxes es poden agafar. Investigar-lo ho veig més per a ESO i si ja s'han treballat i resolt altres jocs anteriorment. Especialment, perquè veig difícil la resolució total. Però la resolució parcial, o l'elaboració de taules com la que proposa en Jordi Font, sí que l'alumnat ho pot fer. Pot ser molt interessant veure les formes de representació que sorgeixin a l'aula.

Com heu vist el procés de resolució pot ser molt ric. I ens pot permetre parlar de l'elaboració de conjectures i de les refutacions d'aquestes. També podem parlar de raonament plausible. I l'aparició dels nombres de Fibonacci té un factor sorpresa important. Si bé és molt possible que per sí sols no arribin a la "norma general", sempre podem oferir alguna pista pel camí. Perquè, per a mi, el que té d'interessant aquesta activitat és el camí més que el destí, i és el que he intentat reflectir durant els dos articles estenent-me tant en la resolució. Sovint parlem d'activitats prou obertes com perquè diferents alumnes arribin a diferents nivells de descobriment. És una de les formes de tractament de la diversitat. Aquest joc permet aquests diferents graus de descobriment. I, de vegades aquestes descobertes es fan en racons del problema com, per exemple, quan intentava descobrir com eren els "nombres problemàtics".

Si heu llegit amb atenció els dos articles veureu com es treballen els quatre processos matemàtics (o les quatre "dimensions", com s'anomenen al currículum) i com es toquen aspectes numèrics i algèbrics interessants. Però, sobre tot, possibilita despertar la curiositat de la descoberta, el motor que pot fer que l'alumnat s'impliqui i, a partir d'aquesta implicació i el seu treball, aprengui matemàtiques. Ens sentirem frustrats per no haver-lo resolt del tot (si és el que passa)? Sincerament, crec que no.