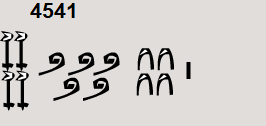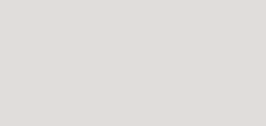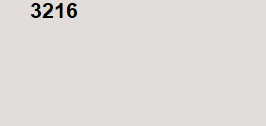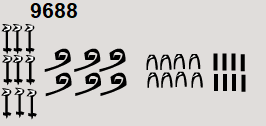"Aquí tens el meu escabot de guies! -va exclamar, mentre amb el llum d'oli il·luminava un feix de bastons d'avellaner, recolzats a la paret en un racó de la cambra-. Veiam si trobem el que tu necessites. Aguanta'm el llumener.
(../..)
Ja el tenim, veus? -va exclamar per fi, mostrant-me un altre bastó-. Aquí ho diu ben clar: Cau del Gel.
Era un gaiato d'uns deu pams de llargària, bigarrat de signes estranys..."
Una possibilitat per indicar el camí en un pal recte és dibuixar un camí Dufour, un tipus de plànol que serveis per indicar itineraris en forma de línia recta.
Vols conèixer com és un itinerari Dufour?