L'algoritme de la multiplicació ha variat força al llarg del
temps. Però en la majoria d'algoritmes que s'han fet servir el que no canvia és
la quantitat de subproductes que hem de fer. Per exemple, si multipliquem 45 ·
738 farem 6 subproductes:
4·700
4·30 4·8 5·700
5·30 5·8
Com que les sumes són més fàcils no les comptem i, considerant
que en realitat cada subproducte és realment de nombres d'una xifra, diem que el
cost d'aquesta multiplicació és 6. Si multipliquem
un nombre de 15 xifres per un altre de 23 el cost
serà de 15·23 = 345 subproductes. En general es considera que el cost de
l'algorisme tradicional de la multiplicació és de n2.
El que és curiós és que el problema de trobar una algoritme millor es continués estudiant
i que, a mitjans del segle XX, s'inventés un altre amb un
cost menor, de forma que, per exemple, una multiplicació de dos nombres de 1000
xifres, que amb els mètodes normals requereix 1 000 000 subproductes, es pugui
resoldre amb poc menys de 60 000.
Quan veiem l'algorisme per primera vegada ens sembla estrany, però en realitat no ho és tant. El va inventar Anatoli Karatsuba a l'any 1962. El mètode demostra tota la seva potència amb nombres molt grans i està pensat per fer els càlculs amb ordinador. Tot i així li podem fer una ullada i podem provar el seu funcionament amb nombres més petits.
I ara pots veure més exemples experimentant amb aquest applet. Pots treballar amb nombres fins a 8 xifres i veuràs que igualem la quantitat de xifres. per fer quantitats parells, afegint zeros a l'esquerra.
 |
| Obrir l'applet (flash) |
Mirem-lo algebraicament
Aquesta part, si no et ve gust veure fórmules, te la pots saltar. Si no és així disfruta amb l'enginy de Karatsuba.
Hem d'imaginar que els dos nombres tenen la mateixa quantitat de xifres n. Ja hem vist que a la pràctica això sempre es pot fer afegint zeros a l'esquerra. Per altra banda n ha de ser parell perquè puguem dividir el nombre en dues parts iguals. Els nombres x i y quedaran dividits en dues parts així:
Fem ara el producte substituïn x i y per les expressions anteriors:
Es pot observar que el primer sumand és el bloc 1 i el tercer el bloc 2. Però el parèntesi del segon sumand no s'assembla al nostre bloc 3. Però podem comprovar que són equivalents:
Aquest truc algebraic per calcular el bloc central (el bloc 3) a partir d'un producte nou i reutilitzant dos anteriors es el que fa reduir la quantitat de subproductes.
Però si en comptes de sumar les dues parts de cada nombre les restéssim el subproducte es faria amb nombres més petits. L'única cosa que haurem de fer és tenir en compte el signe del producte a l'hora de fer els càlculs. Veiem la variant de l'algoritme per trobar el bloc central.
Però si en comptes de sumar les dues parts de cada nombre les restéssim el subproducte es faria amb nombres més petits. L'única cosa que haurem de fer és tenir en compte el signe del producte a l'hora de fer els càlculs. Veiem la variant de l'algoritme per trobar el bloc central.
I ara veiem un parell d'exemples de la variant
Exemple 1. Volem multiplicar 47·82
Exemple 2. Volem multiplicar 2104·3419
Algunes coses més sobre l'algorisme
- Dificultat
 |
| 37 · 52 = 1924 |
 |
| 802 · 4219 = 3383638 |
- Millores de l'algoritme de Karatsuba
Per calcular la multiplicació 57863 · 642307 escrivim, en primer lloc, els dos nombres amb 8 dígits afegint els zeros que calguin. A continuació el descomponem en blocs de 4 i escrivim els tres productes que ens calen, cadascun de quatre xifres. Després repetim el procés fins arribar a productes d'una sola xifra. Com es pot veure tots els productes de nombres de 8 xifres (cost 64 amb la multiplicació normal) és sempre el mateix, 27=33.
Posteriorment a Karatsuba es van fer variacions d'aquest algoritme que encara el milloraven per nombres especialment grans. En concret el de Toom-Cook, del 1963, i el de Schönhage–Strassen, del 1971.
- "Divideix i venceràs"
 |
| Ordenació amb l'algoritme Quicksort |
- Cost
 |
| Gràfic extret de Stoimen's web log |
I a l'aula?
Podem fer diferents coses:
- aplicar l'algorisme a casos senzills.
- atacar el treball algebraic.
- introduir amb aquesta excusa la idea d'eficiència dels algoritmes.
- estudiar costos de casos determinats. Per exemple: quants productes parcials faig amb l'algoritme estàndard per multiplicar dos nombres de vuit xifres? I amb el l'algoritme de Karatsuba sense recursivitat? I amb recursivitat? Per resoldre aquesta qüestió es pot mirar "el pitjor dels casos", quan els nombres són molt grans (com 999999999). Es pot variar la quantitat de xifres i buscar pautes, fórmules per calcular-ho...
Epíleg
Si no volem un resultat superrecontraexacte... què ben inventats estaven els logaritmes, que ens permetien transformar les multiplicacions en sumes!
Altres algoritmes de multiplicació treballats al blog del Calaix +ie
- La multiplicació Veda. Un algoritme que treballa de forma relativament simple amb excessos i defectes.
- Tres algoritmes històrics de multiplicar: piràmide, creueta i fulmínia. Algoritmes relacionats entre sí que es van utilitzar entre els segles XIII i XIX.
- Multiplicar amb dobles o amb dobles i meitats. Les multiplicacions egípcia i russa






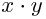












Cap comentari:
Publica un comentari a l'entrada