L'escriptor estatunidenc David Leavitt va escriure al 2007 aquesta novel·la on recrea, entre altres temes, la relació entre els matemàtics Godfred Harold Hardy i Srinivasa Ramanujan, el comptable hindú del títol. No ha estat fins el 2011 que hem disposat d'una traducció al castellà. A l'hora de la veritat el títol és lleugerament enganyós ja que no és Ramanujan l'autèntic protagonista del llibre, la personalitat del qual queda força desdibuixada, sinó que qui focalitzen la narració són Hardy, l'ambient del Trinity College de Cambridge i, en certa manera, la Gran Guerra. Però aquest "petit engany" no treu interès a la novel·la. Si el personatge de Ramanujan queda difús és perquè, fonamentalment, el veiem des de la perspectiva de Hardy, que, amb un caràcter força egocentrista, no està especialment dotat per relacionar-se o comprendre als altres.
És bastant coneguda la història d'aquests dos matemàtics però recordem-la breument. Hardy era un matemàtic amb un cert renom que treballava sovint en col·laboració amb John E. Littlewood. A l'any 1913 va rebre una carta d'una dotzena de pàgines plena de fórmules inusuals signada per un desconegut matemàtic, comptable del Port Trust Office de Madràs i que es declarava autodidacta i . Hardy i Littlewood van saber valorar el treball que se'ls hi presentava i van fer gestions perquè Ramanujan anés a Anglaterra, cosa que van aconseguir. Ramanujan va fer una estada d'uns cinc anys a la Gran Bretanya, just coincidint amb el període de la Primera Guerra Mundial. Va emmalaltir i moria poc després de retornar a l'Índia.
Tenint en compte que parlem de novel·la i no d'història o biografia, la recreació que es fa de l'època i dels seus personatges, dels seus dilemes, de les seves contradiccions és interessant.
I les matemàtiques tenen una presència, no només inevitable, sinó intencionadament clara. I un dels problemes que del que es parla de forma més reiterada és el de les particions, un problema encara no resolt de forma completa i que té un plantejament que es pot explorar perfectíssimament des de l'educació primària.
Vols conèixer el problema a de les particions?
Llegim el text del llibre:
El plantejament del problema és clar: "de quantes maneres podem dividir un nombre?". El text de la novel·la ens mostra de forma clara que, a mesura que aquests van creixent, la quantitat corresponent de particions es dispara de forma ràpida. A la següent imatge podem veure les set formes en que podem partir el 5 cigrons (canviem de llegum).
 |
| Hardy i Ramanujan |
I les matemàtiques tenen una presència, no només inevitable, sinó intencionadament clara. I un dels problemes que del que es parla de forma més reiterada és el de les particions, un problema encara no resolt de forma completa i que té un plantejament que es pot explorar perfectíssimament des de l'educació primària.
Vols conèixer el problema a de les particions?
Llegim el text del llibre:
"Ramanujan está echando la cúrcuma en un cuenco con una cuchara. Las lentejas del rasam reposan en otro cuenco. Al quitarles las piedrecitas con la punta de los dedos, tal como su madre le enseñó a hacer, se le caen unas cuantas sobre la superficie de la mesa. Mientras las junta barriéndolas con la mano, las cuenta. Siete lentejas. ¿De cuántas maneras se pueden dividir siete lentejas? Bueno (hace la prueba), se pueden dividir en siete partes de una cada una, o en una de seis y una de una, o en una de cinco y dos de una, o en una de cinco y una de dos, o en una de cuatro y una de tres, o en una de cuatro y una de dos y una de una, o en tres de dos y una de una, o...
Quince en total. Sí, se pueden dividir siete lentejas de quince maneras distintas.
¿Y de cuántas maneras se pueden dividir ocho lentejas? Saca con cuidado una lenteja del cuenco y la pone sobre la mesa con las otras.
Ocho partes de una cada una, una de siete y una de una, una de seis y una de dos, una de seis y dos de
una ...
Veintidós maneras. ¿Y nueve?
Treinta maneras.
Sigue calculando. No come. Ya son más de las doce cuando ha conseguido averiguar el número de maneras en las que se pueden dividir veinte lentejas, y para entonces hay lentejas por todos lados, en el suelo y debajo del hornillo. Pronto descubrirá que algunas han emigrado hasta su cama. Se agarran a las fibras de la bufanda que le ha hecho el famoso escritor. Todo este año su señora de la limpieza se las encontrará en el recogedor cuando barra. Y en 1994, un estudiante de ingeniería de Yakarta, intentando recuperar una lentilla perdida, sacará una de una rendija entre las tablas del suelo.
El rasam sigue sin hacerse. Seiscientas veintisiete maneras."
El plantejament del problema és clar: "de quantes maneres podem dividir un nombre?". El text de la novel·la ens mostra de forma clara que, a mesura que aquests van creixent, la quantitat corresponent de particions es dispara de forma ràpida. A la següent imatge podem veure les set formes en que podem partir el 5 cigrons (canviem de llegum).
És interessant explorar els primers casos, tot procurant no deixar-nos-en cap. És una tasca abordable perfectament per alumnat primària. A una taula podem anar recollint resultats:
| Nombre | Particions | Total de particions |
| 1 | (1) | 1 |
| 2 | (2) (1+1) | 2 |
| 3 | (3) (2+1) (1+1+1) | 3 |
| 4 | (4) (3+1) (2+2) (2+1+1) (1+1+1+1) | 5 |
| 5 | (5) (4+1) (3+2) (3+1+1) (2+2+1) (2+1+1+1) (1+1+1+1+1) | 7 |
| 6 | (6) (5+1) (4+2) (4+1+1) (3+3) (3+2+1) (3+1+1+1) (2+2+2) (2+2+1+1) (2+1+1+1+1) (1+1+1+1+1+1) | 11 |
| 7 | (7) (6+1) (5+2) (5+1+1) (4+3) (4+2+1) (4+1+1+1) (3+3+1) (3+2+2) (3+2+1+1) (3+1+1+1+1) (2+2+2+1) (2+2+2+1) (2+2+1+1+1) (2+1+1+1+1+1) (1+1+1+1+1+1+1) | 15 |
| 8 | (8) (7+1) (6+2) (6+1+1) (5+3) (5+2+1) (5+1+1+1) (4+4) (4+3+1) (4+2+2) (4+2+1+1) (4+1+1+1+1) (3+3+2) (3+3+1+1) (3+2+2+1) (3+2+1+1+1) (3+1+1+1+1+1) (2+2+2+2) (2+2+2+1+1) (2+2+1+1+1+1) (2+1+1+1+1+1+1) (1+1+1+1+1+1+1+1) | 22 |
| ... | ... | ... |
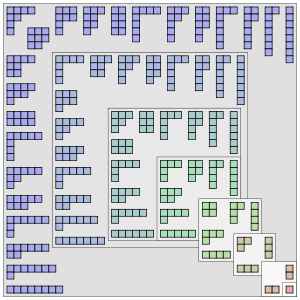
A continuació teniu una bonica representació gràfica de totes aquestes particions.
Com veiem cada vegada és més fàcil deixar-se algun cas. Per exemple, el nombre 25 ja té 1958 particions, el 100 més de 190 milions, 200 s'acosta als 4 bilions i 1000 ronda el 24 quintilions. La sèrie que dóna la quantitat de particions a un nombre n és la OEIS A000041.
Hardy i Ramanujan no van aconseguir una fórmula que donés exactament la quantitat de particions de un nombre n, el que anomenarem p(n). Però sí algunes que s'aproximaven molt. La millor és aquesta en la que només cal arrodonir a l'enter més pròxim.
Una altra, més fàcil de manejar però més inexacta i que dóna valors més bon a mesura que n es va fent més gran, és la següent.
Una altra, més fàcil de manejar però més inexacta i que dóna valors més bon a mesura que n es va fent més gran, és la següent.
És sorprenent trobar-nos al vells amics e i Π barrejats en ella!
Un vell i bell problema fàcil de plantejar i complicadíssim de resoldre. I una història a comentar a classe.





Cap comentari:
Publica un comentari a l'entrada