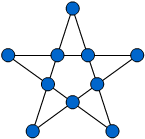
El tauler de joc és una estrella de cinc puntes sobre la que es col·loquen 10 fitxes.
Vols estudiar el joc?
1) Busquem "finals"
Per estudiar molt jocs una bona tàctica és començar per observar les posicions finals. Això ho fan molt alumnes de forma natural: juguen una mica "a la babalà" al començament i quan queden poques fitxes es paren a "pensar".
Si els demanem, en petits grups, que ens diguin "posicions guanyadores" (situacions de la partida que si se les deixes al contrari no tindrà res a fer, estarà "perdut") ràpidament ens diran aquestes primeres.
1) Busquem "finals"
Per estudiar molt jocs una bona tàctica és començar per observar les posicions finals. Això ho fan molt alumnes de forma natural: juguen una mica "a la babalà" al començament i quan queden poques fitxes es paren a "pensar".
Si els demanem, en petits grups, que ens diguin "posicions guanyadores" (situacions de la partida que si se les deixes al contrari no tindrà res a fer, estarà "perdut") ràpidament ens diran aquestes primeres.
 |
| Deixar dues separades (1-1) |
 |
| Deixar quatre separades (1-1-1-1) |
 |
| Deixar dues parelles separades (2-2) |
Els dos primers casos són força evidents ja que fan una alternança TU-JO que acaba en JO. El tercer cas també és fàcil: si el contrari agafa una, nosaltres agafem una també de l'altra parella; si n'agafa dues, nosaltres agafarem les dues que queden.
2) Fem "un pas enrere"
Ara tocaria proposar un repte una mica més gran: estudiar posicions anteriors que es puguin reduir a uns d'aquests casos. Per exemple una altra posició guanyadora no gaire difícil de descobrir és aquesta en la que queden dues ternes de fitxes.
 |
| (3-3) |
Per poc que s'estudiï es pot observar que per a qualsevol acció del contrari puc deixar-lo en una de les tres primeres posicions estudiades (1-1, 1-1-1-1 o 2-2).
Aquest és un altre moment en el que convé treballar cooperativament amb el grup gran, amb tota la classe. Es tracta de fer una col·lecció àmplia de posicions guanyadores que podem classificar segons la quantitat de fitxes en joc: 4, 5, 6... Polir la col·lecció evitant repeticions és també un exercici interessant en el que intervindran agrupacions similars, girs, simetries... que caldrà descobrir.
Un cas d'equivalència dels més senzills d'observar és el següent en que tenim dues ternes de fitxes separades.
Però segur que entre els alumnes serà un bon motiu de discussió en els que uns hauran de construir bons arguments per convèncer als altres, especialment segons l'edat amb la que s'estigui treballant.
A continuació teniu un col·lecció de posicions guanyadores per a 4, 5, 6 i 7 fitxes. Especialment per a les de 6 i 7 cal mirar com, per a cada jugada del contrari, tenim una resposta que ens porta a una posició guanyadora més simple:
 |
| Es pot observar que les posicions a, b, c, f i g tenen en comú tenir un triangle a una punta de l'estrella i dues fitxes més |
3) Estudiem les sortides
Fins ara hem estudiat finals i "semifinals". Potser que ara ataquem els començaments. Si preguntem a classe quantes sortides diferents hi ha, quantes "primeres jugades" distintes pot fer el primer jugador (el que obre el joc) segur que tindrem una altra discussió interessant: són 10 perquè hi ha 10 fitxes? Són 20 perquè pot sortir amb una o dues fitxes? Es pot reduir aquesta quantitat tenint en compte les simetries i girs?
Si ho estudiem amb calma veurem que només hi ha quatre sortides totalment diferents possibles:
4) Definim l'estratègia! (per tres de les sortides)
Podem estudiar sortida per sortida. La més complexa, com veurem, és la primera, l'A. Podem repartir per grups l'estudi de les sortides B, C i D que són les més directes. El repte a proposar és el següent: podem convertir directament la sortida que t'ha correspost en una de les"nostres posicions guanyadores"?
Es pot observar que sí i que, per aquestes sortides, seria el segon jugador (el que no comença) qui guanyaria la partida. Per identificar la resposta ho fem de la següent manera: 6-b significa que la posició està marcada amb la lletra b a les del grup de 6 fitxes de la nostra col·lecció anterior.
5) Definim l'estratègia! (per la sortida que falta: A)
Aquesta sortida és la que dóna més "guerra" perquè a la nostra llista de posicions guanyadores no tenim cap amb 8 fitxes ni una immediata de 7. A la primera versió d'aquesta entrada mostrava una estratègia guanyadora errònia per oblidar estudiar una de de les possibles respostes a la que em pensava que era la jugada guanyadora per al segon jugador. Gràcies al mateix Jordi Deulofeu i a un escrit que m'ha enviat de Xavier Valls ja l'he pogut subsanar. Cal dir que aquestes coses passen i més si el joc s'estudia sol: quatre ulls veuen més que dos i l'estudi col·laboratiu que plantegem pot ajudar a evitar-lo.
Per altra banda... hem fet una recerca exhaustiva de posicions guanyadores? La veritat és que jo no. Només he anotat algunes de les que he anat trobant. És possible que a la classe hagin sortit més, però també és possible que no. En tot cas, treballant col·laborativament, s'han d'anar fent passes endavant i endarrere. Per exemple, a partir d'una posició un dels jugadors perd. Llavors s'ha de revisar la darrera jugada, reconstruir la situació i provar-ne una altra opció. I anar fent i desfent per esgotar les possibilitats. Només així podrem decidir si una determinada situació de joc és guanyadora o perdedora.
En el nostre cas, per la sortida A (una fitxa d'una punta) no tenim resposta directa encara. És l'única opció perquè el primer jugador disposi d'una estratègia guanyadora, ja que les altres sortides (B, C i D) determinen una estratègia pel segon. Provant i provant podem trobar-ne una de nova, amb 8 fitxes, que encara no havíem provat i que ens diu que el segon jugador també té una resposta guanyadora.
Per no fer una diagrama en arbre molt gran el dividirem en tres parts per veure com el segon jugador pot aconseguir posicions guanyadores. No indiquem totes les branques possibles perquè alguns casos els podem deduir directament de les posicions que tenim inventariades abans.
Sortides del 1r amb una fitxa
Sortides del 1r amb dues fitxes del pentàgon interior
Sortides del 1r amb dues fitxes: una exterior i una interior
Conclusió
Aquest joc té una estratègia guanyadora per al segon jugador. Per a cada jugada que el primer jugador faci, si ens guiem per la nostra llista de posicions guanyadores, trobarem una resposta que ens portarà a situacions avantatjoses. I aquesta llista l'haurem construït entre tots els nens i nenes, nois i noies, de la classe.
Us animeu a posar-lo en pràctica?














Cap comentari:
Publica un comentari a l'entrada