Recordem el problema: "Quina és la longitud del segment paral·lel a les bases d'un trapezi isòsceles que el divideix en dues parts amb la mateixa àrea?". No tenim les dades sobre l'altura.
A més, podem observar que l'altura del trapezi no hi compta per res. És indiferent l'altura que tingui, el segment de tall sempre tindrà la mateixa longitud.
Per altra banda tampoc cal que el trapezi sigui isòsceles. La propietat serveix per a tots.
Voleu veure les dues solucions noves?
- Solució Alsina-Aubanell
L'Anton Aubanell va explicar aquesta solució a la conferència que va realitzar sobre visualització matemàtica (“Geometria per visualitzar, experimentar, interpretar, raonar… un repte!”) a la XII Jornada de l'Ensenyament de les Matemàtiques (3/10/15 a l'IEC). A la imatge el veient mostrant els dos trossos del trapezi equilibrats, com en una balança, per il·lustrar la igualtat d'àrees.
Segons ens va explicar la solució li va passar en Claudi Alsina. Mirem-la.
El que proposen és allargar els costats no paral·lels del trapezi per formar un triangle. La figura obtinguda ja ens convida a pensat en aplicar el teorema de Tales.
A continuació s'estableixen relacions de proporcionalitat però una mica diferents de les habituals. Les proporcions les farem entre àrees i longituds, tenint en compte que les raons de proporcionalitat de les longituds s'han d'elevar al quadrat. Recordem: un rectangle de costats dobles té el quàdruple d'àrea (22); un triangle al que se li tripliquen els costats té un augment d'àrea a nou vegades l'original (32).
A la figura podem observar tres triangles. El V de color verd i d'àrea desconeguda; li direm "triangle petit". El format per aquest mateix triangle i la meitat superior del trapezi (d'àrea V+A); li direm "triangle mitjà". I, finalment, el "triangle gran", el més gran, format pel triangle verd i els dos mitjos trapezis (d'àrea V+2A).
Podem establir dues igualtats basades en les proporcions entre àrees i els segments a, b i x. El triangle petit i el mitjà tenen la mateixa proporció que el quadrat de la raó entre els costats corresponents b i x. El triangle gran i el mitjà tenen la mateixa proporció que el quadrat de la dels costats corresponents a i x. Amb això podem muntar un sistema d'equacions:
Amb GeoGebra podem experimentar tot el que hem vist.
A la figura podem observar tres triangles. El V de color verd i d'àrea desconeguda; li direm "triangle petit". El format per aquest mateix triangle i la meitat superior del trapezi (d'àrea V+A); li direm "triangle mitjà". I, finalment, el "triangle gran", el més gran, format pel triangle verd i els dos mitjos trapezis (d'àrea V+2A).
Podem establir dues igualtats basades en les proporcions entre àrees i els segments a, b i x. El triangle petit i el mitjà tenen la mateixa proporció que el quadrat de la raó entre els costats corresponents b i x. El triangle gran i el mitjà tenen la mateixa proporció que el quadrat de la dels costats corresponents a i x. Amb això podem muntar un sistema d'equacions:
Ara només toca resoldre'l i veurem com la dada desconeguda (V) desapareix.
Aïllant la x arribem a la solució que havíem dit al començament i que es coneix com a mitjana quadràtica.
Encara, però, hi va quedar un "rum-rum". La solució encara s'havia de poder arrodonir geomètricament reduint el pes de àlgebra. És aquí quan apareix la solució d'en Josep Rey.
En aquest primer apartat només cal afegir que, a la conferència, l'Anton va estendre el problema per a un tronc de piràmide per fer-nos veure que, en aquest cas, s'ha d'utilitzar la mitjana cúbica per solucionar el problema. Per "mostrar-ho" va tallar un formatge en forma de tronc de piràmide i va pesar les dues parts fent observar que pesaven el mateix.
En aquest primer apartat només cal afegir que, a la conferència, l'Anton va estendre el problema per a un tronc de piràmide per fer-nos veure que, en aquest cas, s'ha d'utilitzar la mitjana cúbica per solucionar el problema. Per "mostrar-ho" va tallar un formatge en forma de tronc de piràmide i va pesar les dues parts fent observar que pesaven el mateix.
- Solució de Josep Rey
El primer esquema, que no manté proporcions i ens ajudarà a visualitzar la situació és el següent:
En aquest dibuix veiem el nostre trapezi original de bases "vermella" i "blava" dividit en dues parts per un segment "verd", del qual en busquem la mida. S'ha afegit un triangle blau que més tard ens serà útil i que, de moment, ens ajuda a pensar en l'ús de la proporcionalitat geomètrica.
Amb el segon esquema ens planteja l'enunciat del problema: dues vegades un dels trapezis de bases més petites ("verda" i "blava") té la mateixa àrea que el trapezi original.
En el tercer dibuix afegeix els dos triangles als dos trapezis anterior i, per mantenir la igualtat, afegeix també dos triangles a l'altre costat, un col·locat sobre el trapezi original i l'altre solt.
Ara intervé una idea clau. Aquestes proporcions entre àrees, si mantenim les longituds bàsiques, seran independents de les figures concretes. El que ve és un pas difícil de veure. L'heu de rumiar. Si mireu la següent imatge "veureu" que les tres parelles de figures són semblants. A cada parella la proporció entre l'àrea del triangle i la del quadrat és igual i, en conseqüència. les proporcions entre les àrees dels tres triangles entres sí són idèntiques a les que mantenen les àrees dels quadrats.
Podem substituir els dos triangles de l'esquerra, de base "verda", per dos quadrats de costat "verd". També haurem de substituir el triangle de base "vermella" per un quadrat de costat "vermell" i el triangle de base "blava" per un quadrat de costat "blau". La igualtat no es trenca.
Podem substituir els dos triangles de l'esquerra, de base "verda", per dos quadrats de costat "verd". També haurem de substituir el triangle de base "vermella" per un quadrat de costat "vermell" i el triangle de base "blava" per un quadrat de costat "blau". La igualtat no es trenca.
Quan "val" la suma dels dos quadrats de la dreta? Cap problema. El teorema de Pitàgores ens dóna la solució.
El nostre quadrat verd és, per definició de l'enunciat, la meitat del quadrat negre. No és difícil dibuixar-lo convenientment en aquest quadrat suma construït sobre la hipotenusa.
Recordem: els segments blau i vermell són les bases del nostre trapezi original. El segment verd és el segment solució.
Ja ho tenim! El segment que busquem és equivalent al costat del quadrat que té la meitat d'àrea que la suma dels quadrats de les bases. És el que algebraicament hem trobat abans.







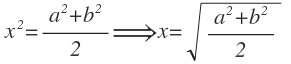












Gràcies, Joan!
ResponElimina