 |
| Imatge treta d'un article de D. Chavey |
 |
| Sona d'una (4x3), dues (6x4) i cinc trajectòries (5x5) |
Si no vols que fem espòiler millor que deixis de llegir ara mateix i te'n vagis al primer l'article sobre els lusona. Allà trobàvem la pauta sobre la quantitat de trajectòries.
Però, en aquell article, vam deixar pendent el perquè. I d'això és del que volem parlar ara: per què la quantitat de trajectòries ve determinada pel m.c.d. dels costats?
Però, en aquell article, vam deixar pendent el perquè. I d'això és del que volem parlar ara: per què la quantitat de trajectòries ve determinada pel m.c.d. dels costats?
No farem una demostració formal completa sinó que aportarem les idees fonamentals que es basen en veure la descomposició d'un sona en subsones quadrats idèntics i en l'estudi de les propietats dels sona quadrats. Si voleu veure una demostració completa (de la que hem tret la majoria d'idees que aquí s'expliquen) podeu llegir la publicada Manuel García Piqueras a la Gaceta de la RSME.
Canviem el dibuix base
Canviem el dibuix base
Els dibuixos de sona que hem mostrat abans eren una simplificació en la que eliminàvem els punts interiors i assenyalàvem uns punts exteriors de reflexió de la trajectòria.
És una simplificació que a l'aula va bé perquè al principi costa una mica que les trajectòries es dibuixen bé. Els rebots de "taula de billar" costen una mica d'entendre si no vigilem molt de que el "camí" vagi ben bé per les diagonals de la quadrícula de suport.
Aquesta vegada tornarem a recuperar els punts interiors, però no tots: només els que marquen la trama principal. Encara que per comptar parlarem sempre de punts veurem que la distància entre dos punts consecutius de la trama serà sempre de dos quadrets de la quadrícula de suport. També marcarem a l'exterior el rectangle on "rebota" la trajectòria.
 |
| Transformació de l'esquema |
Estudiem el cas 9x3
Si dibuixem una de les trajectòries d'una una trama de 9x3 obtindrem el següent dibuix:
Com veiem si el "costat" no és dels exteriors, on s'ha de rebotar, sempre passem a un quadrat del costat. Però el trajecte aviat es començarà a creuar. Creuar-se implica passar per uns dels vèrtexs dels quadrats petits pels que ja hem passat, però en una direcció que no havíem dibuixat pel fet "d'haver-nos escapat".
Si dibuixem una de les trajectòries d'una una trama de 9x3 obtindrem el següent dibuix:
No és difícil veure tres rectangles inclinats similars. De fet, si descomponem el rectangle en tres quadrats de 3x3 veurem que el dibuix s'aconsegueix aplicant dues simetries verticals successives del primer quadrat.
Obtenim un resultat semblant si completem el dibuix amb un segona trajectòria.
La tercera trajectòria necessària per envoltar tots els punts tampoc provoca canvis transcendentals.
Podríem dir que un lusona de 9x3 està compost per la unió de tres sones de 3x3. Dos "subsona" units per un costat són simètrics.
Un lusona de 9x6
Aquesta sèrie de dibuixos, seguint un ordre com el de l'anterior cas, ens mostra que un lusona de 9x6 també està format per subsones més petits de 3x3 i units amb un patró similar de simetries.
Un lusona de 10x4
En aquest cas veiem que el subsona reduït quadrat que tenim dins és de 2x2
... I en general...
...veiem que tots els sona es poden descompondre en una quantitat mínima de subsones més petits quadrats. La quantitat mínima ens la dona el màxim comú divisor dels dos costats. En el cas de que els dos costats de la trama siguin primers entre si els quadrats mínims seran d'1x1.
No ho tenim tot encara. Una altra observació.
Hem vist que qualsevol lusona els podem descompondre en subsones quadrats idèntics i que la quantitat de subsones quadrats ve marcada pel m.c.d. dels costats de la trama de punts. Ara bé... una cosa són els subsones i una altra les trajectòries. Ens falta buscar un enllaç entre les dues idees.
L'enllaç ens el donarà l'estudi de les propietats dels sona quadrats.
Una de les primeres observacions que podem fer és que un lusona quadrat té tantes trajectòries com indica el seu costat. També que cap de les trajectòries es pot subdividir en altres més petites. De fet, i això és important, cada trajectòria té quatre vèrtexs i cadascun dels vèrtexs toca un costat diferent del quadrat gran.
Podem veure perquè cada trajectòria rebota successivament als quatre vèrtexs. És inevitable. Una línia que neixi en un costat anirà a tocar un dels costats contigus. Tenim cinc segments possibles en quant a longituds que, mirant en diagonal, "freguen" un, dos, tres, quatre o cinc punts. Aquests segments van associats, en els rebots, de dos en dos 1-5 i 2-4, 3-3. Per exemple, a un segment de 2 li seguirà un rebotat de 4, a aquest un de 2 i a aquest un de 4 tancant el rectangle.
D'aquesta forma es produeixen els cinc tipus de rectangles "inclinats", que hem vist abans, amb un vèrtex a cada costat.
I ara ho unim tot
El que ens queda és unir les dues idees que tenim:
- cada lusona es pot dividir en quadrats més petits amb un costat igual al m.c.d. dels dos costats del rectangle que el forma.
- en un quadrat hi ha tantes trajectòries com punts té el costat i en una trajectòria es toquen successivament els quatre vèrtexs.
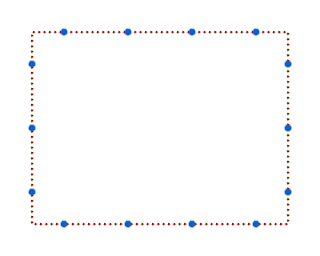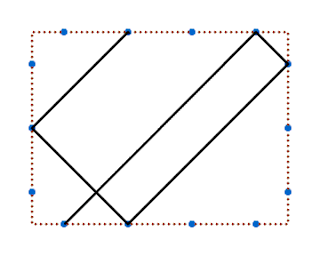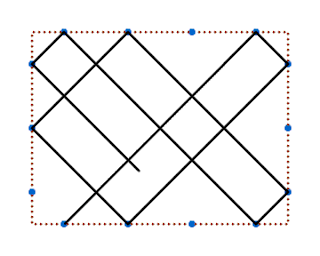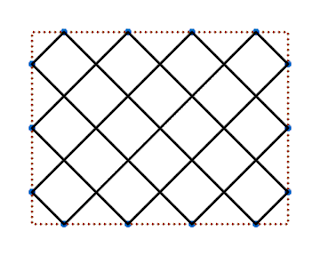
En primer lloc marquem els quadrats dels subsones que el formaran i que seran de 3x3
Comencem a fer una línia d'un dels subquadrats, sortint d'un costat, fins que toqui el següent.
Si només tinguéssim el quadrat el segment rebotaria en diagonal cap a l'esquerra i cap amunt, però ara es pot escapar per la dreta fent un segment simètric a l'altre quadrat.
Aquest nou segment, si no pogués sortir del quadrat rebotaria, però té un escapament cap al quadrat superior fent un altre segment simètric al que s'hauria dibuixat a l'interior.
Al quadrat que entra ara la línia, pel fet de tocar dos laterals exteriors, pot fer 2 rebots i escapar-se al pel quadrat inferior.
Quadrat a quadrat, costat a costat d'aquests quadrats, s'aniran construint rectangles de la mateixa forma fins a tancar el recorregut.
Començant per un altre punt construiríem un altre joc de rectangles. I un cop acabat aquest itinerari podríem fer el que falta. I un cop acabat aquest itinerari podríem fer el tercer que ens falta.
I així ja tenim construït tot l'argumentari bàsic per justificar perquè la quantitat de trajectòries d'un lusona és el m.c.d. dels costat de la trama.
... i un vídeo
Per acabar, i per veure la bellesa de com es dibuixen, us deixem un vídeo on es veu com fer un lusona més artístic. Aquest seria un lusona amb miralls, dels que vam parlar al primer article.




















Cap comentari:
Publica un comentari a l'entrada