Heptatrisecció de l'angle

A l'antiga Grècia, per resoldre els problemes geomètrics, es van autoimposar un regles de joc. De la mateixa manera que quan juguem a futbol, si no som porters, ens autoimposem no tocar la pilota amb els braços encara que ho puguem fer amb qualsevol altra part del cos, les regles gregues per a la resolució de problemes es referien a les eines a utilitzar: només rectes i circumferències, o, dit d'una altra manera, amb regle sense graduar i compàs col·lapsable (un compàs que es tanca quan el separes del paper). Van resoldre molts problemes, però hi ha tres que van passar a la història perquè no en van trobar la solució:

• la quadratura del cercle (construir un quadrat d'àrea equivalent a un cercle donat).
• la duplicació del cub (trobar l'aresta del cub de volum doble a un altre donat).
• la trisecció de l'angle. 

Segles més tard es va demostrar que cap dels tres problemes era resoluble amb aquestes regles de joc. Potser del que menys es parla és el de la trisecció de l'angle i, per aquest motiu, li dedicarem aquest article.

Una dels teoremes més bonics relacionats amb la trisecció de l'angle és el teorema de Morley. Aquest teorema diu que els punts d'intersecció entre les trisectrius dels angles d'un triangle qualsevol formen un triangle equilàter. Pots provar-ho amb aquest applet.

És evident que hi ha angles concrets, com el de 90º, que es poden trisecar amb regles i compàs. Us convidem a fer-ho amb GeoGebra.

https://www.geogebra.org/m/z32rpRP2

Però la impossibilitat de la resolució del problema general, per a qualsevol angle, va ser demostrada per  Pierre Wantzel al 1837. Si bé a l'antiga Grècia no van saber resoldre el problema amb regle i compàs de forma exacta, sí que ho van saber fer amb altres eines. Per exemple amb un regle amb un parell de marques o amb regle, compàs i algunes corbes especials com l'espiral d'Arquímedes, la quadratriu d'Hipies o la concoide de Nicomedes. Són solucions molt boniques que es poden mostrar i treballar a l'aula. Recordem que la cultura matemàtica, i en concret el coneixement de la seva història, han de ser part important del bagatge dels nostres alumnes.

Espiral d'Arquimedes

Quadratiu (o trisectriu) d'Hipies

Concoide de Nicomedes

També mostrarem un trio d'artefactes mecànics que trisequen l'angle: els trisectors de Ceva, Laisant i Kempe.

Pantògraf de Ceva

Trisector de Laisant

Trisector de Kempe

Ens hi posem?

• Un mètode d'Arquímedes

Imaginem que ens està permès fer un parell de marques al regle. El procediment per trisecar un angle consistirà en seguir aquestes passes:

• Tracem una semicircumferència amb el centre al vèrtex de l'angle que volem trisecar.
• Allarguem un dels costats construint una recta que ens farà de base
• Marquem al regle un segment amb la mesura del radi de l'arc traçat.
• Col·loquem el regle de forma que un dels extrems del segment coincideixi amb la línia base i l'altre amb l'arc de la semicircumderència.
• L'angle que formen aquesta recta i la base és 1/3 del primer angle.

Podem comprovar-ho amb aquesta construcció amb GeoGebra. Movent el punt A variem l'angle i fent-ho amb el B podem col·locar el segment en la posició demanada.

Proposta: podeu demostrar per què?

• L'espiral d'Arquimedes

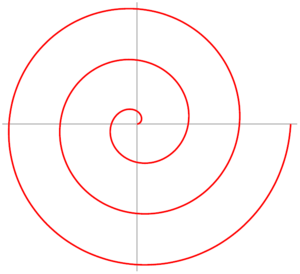
Arquimedes encara es va un altre regal trisecador a banda del mètode anterior utilitzant "la seva" espiral. Una espiral és arquimediana si la separació entre les voltes és constant. Arquimedes, que la va estudiar en profunditat al seu tractat De les línies espirals, ens va explicar com utilitzar-la per trisecar l'angle.

• Col·loquem l'angle sobre l'eix horitzontal de l'espiral.
• Busquem el punt on es tallen l'altre costat de l'angle i l'espiral.
• Dividim el segment format en tres parts iguals.
• Tracem tres arcs amb centre al vèrtex de l'angle que surtin dels punts obtinguts.
• Obtenim dos punts nous de tall amb l'espiral que ens assenyalen la direcció de les rectes trisectrius.

Ho podeu comprovar amb aquest applet.

Hem de reconèixer una gran bellesa matemàtica en aquests connexió sorprenent entre una corba com l'espiral i el problema de la trisecció.

Propostes: hi ha altres tipus d'espirals? Podem trobar exemples d'espirals d'Arquimedes a l'entorn?

• La quadatrix d'Hipies

Aquesta corba la va descriure Hipies d'Elis al segle V a.n.e. molt abans de l'estudi d'Arquimedes sobre "la seva espiral" o de l'estudi de les còniques. També serveix, sorprenentment, per trisecar l'angle. êrò primer hem de descriure com es construeix aquesta corba.

Imaginem que tenim un quadrat amb un quart de circumferència a l'interior. Aquest arc té el radi igual al costat i el centre a una dels vèrtexs. A continuació imaginarem dos moviments simultanis:

• el costat superior va baixant, amb velocitat constant, fins a arribar a coincidir amb el costat oposat inferior.
• el costat esquerra (el radi de l'arc) va girant, també amb velocitat constant, sobre el vèrtex fins arribar també al costat base.
• els dos moviments es fan en un mateix temps: arrenquen i arriben a la vegada.

La corba d'Hipies, que anomenem quadratrix, és "el rastre" del punt de tall del segment i el radi. I si dividim en tres parts els tros que li queda al segment que s'està movent fins a la base i fem dues paral·leles a aquesta obtenim dues interseccions amb la quadratrix que trisequen l'angle format pel radi amb la base.

Ho podeu comprovar amb aquesta construcció. Podeu moure el radi el segment utilitzant el punt lliscant. També podeu activar la animació amb el botó de la part inferior esquerra.

Construcció base de l'applet de Manuel Sada

Podeu trobar una demostració sobre la divisió de l'angle amb aquesta corba i sobre com utilitzar-la per quadrar el cercle (demostració inclosa) al web de Gaussianos.

• La concoide de Nicomedes

Ara viatgem al segle III a.n.e. Nicomedes, un matemàtic grec del que sabem ben poc, va escriure un tractat sobre les concoides on descrivia com aquestes corbes resolien la trisecció de l'angle.

Com abans, hem de mirar com es construeixen. Una primera opció és que mireu i analitzeu la següent imatge. (La podeu "animar" clicant sobre ella)

Una altra és seguir la següent descripció:

• sobre una recta assenyalem dos punts i dibuixem dues circumferències iguals que els tinguin per centre.
• a una d'elles marquem un punt i tracem la recta que l'uneix a l'altre centre
• aquesta recta s'interseca aquesta circumferència en dos punts
• si movem sobre la recta aquesta segona circumferència els punts d'intersecció aniran ocupant diferents posicions. El conjunt d'aquestes posicions (el lloc geomètric) defineix la concoide de Nicomedes.

Podeu experimentar diferents formes de la concoide movent els punts B i C.

I ara mirem com la podem utilitzar  per trisecar l'angle.

• Tracem la recta que uneix el punt sobre la primera circumferència (el que defineix l'angle a trisecar) amb la intersecció d'aquesta circumferència amb la concoide.
• L'angle que forma aquesta recta amb la "recta base" és la tercera part de l'altre.

---

Mecanismes trisectors

Comencem ara ha descriure alguns aparells mecànics per trisecar l'angle. Venen a ser una mena de compassos o pantògrafs que es tracten de triplicar una angle. Això permet que es puguin utilitzar a la inversa, dividint-lo en tres parts iguals. En tots ells és interessant mirar el joc dels angles dels mecanismes: quin es repliquen i on, quins e modifiquen i com...

• El pantògraf trisector de Ceva

El seu inventor va ser el matemàtic italià Giovanni Ceva a l'any 1696 (encara que algunes fonts l'atribueixen al seu germà Tomasso). Aquest matemàtic va investigar uns corba, la trisectriu o cicloide de Ceva força interessant també per seu disseny i que també triseca l'angle. Per veure com funciona el pantògraf de Ceva només heu de moure els punts vermells. Observareu que hi ha quatre punts articulats i dos, als extrems, que llisquen sobre la recta. Aquesta recta, al pantògraf real, és una mena de guia.

Proposta: demostreu geomètricament per què es triplica l'angle.

• El trisector de Laisant

Aquest mecanisme va ser inventat pel matemàtic francès Charles-Ange Laisant al 1875. A diferència de l'anterior, la trisecció comparteix vèrtex amb l'angle que volem trisecar. Aquesta simulació en GeoGebra no és prou polida com per simular perfectament el mecanisme, però ens pot servir per fer-nos una idea de com funciona. Els punts vermells llisquen sobre unes barres i la resta estan articulats. Podem moure el punt vermell gran per variar l'angle.

Proposta: per què es mantenen els tres angles iguals?

• El pantògraf de Kempe

Aquest pantògraf va ser inventat per Alfred Bray Kempe al 1876.  Abans de presentar-vos una simulació mireu un petit vídeo agafat de la pàgina russa Трисекция угла (Estudis matemàtics). Podeu visitar la pàgina amb tranquil·litat ja que tenen versions en anglès, italià i francès. En aquest vídeo s'explica visualment com construir el pantògraf i la base matemàtica, ja que ens van mostrant elsangles que es conserven. Primer es construeix un bisector i, a continuació, un trisector.

Ara sí podeu veure'l en aquesta simulació construïda per milanoff. Podem variar els angles movent els punts B, C o A.

• Epíleg

Com sempre no hi ha res que no hagi explicat Martin Gardner alguna vegada. El teorema de Morley apareix al llibre Nuevos pasatiempos matemáticos (capítol 17, titulat H.S.M. Coxeter). Al "Carnaval matemático" va dedicar tot un capítol a la trisecció de l'angle: el 19 Cómo trisecar un ángulo.

Però el mateix Gardner cita un llibre italià del 1913, Matematica dilettevole e curiosa, d'Italo Ghersi i que us recomanem de cor. A Itàlia en cara es va editant (Editorial Hoepli). En aquest llibre hi trobareu 14 solucions basades en corbes de diferents tipus i 20 de mecàniques.

 Curiosament ni Gardner ni Ghersi parlen de la corba d'Hipies (que, com hem dit abans serveix també per quadrar el cercle). Aquesta corba la vaig trobar per primera vegada en un llibre d'en Lluís Segarra: Els millors problemes (Edicions de la Magrana).

I si no en teniu prou només heu de cercar a Google o Yotube. No us ho acabareu en dos dies.

I una propina circense

Malgrat la demostració inapel·lable de la impossibilitat de la trisecció de l'angle amb regle i compàs com passa moltes altres vegades els mitjans de comunicació mostren un total aculturalisme sobre aquesta qüestió. Si més no per desconèixer què significa, en matemàtiques, que una cosa està demostrada. A l'estiu de l'any 1996 el diari El País publicava un article amb aquest text:

"EL MATEMATICO DEL CIRCO. Luis Raluy Tomás, dueño del circo de tinte clásico Raluy, realizó ayer ante los medios de comunicación el número más espectacular de su carrera. Formado libremente en las teorías matemáticas entre gira y gira, Raluy demostró con un compás y una regla la posibilidad de trisecar un ángulo, una de las grandes cuestiones irreso-lubles de las llamadas ciencias exactas. Un carromato de principios de siglo fue el escenario elegido por Luis Raluy, hijo del famoso hombre cañón, para dividir un ángulo en tres partes iguales ante los atónitos periodistas. Ni Pitágoras consiguió desentrañar esta cuestión que fue zanjada en 1837 y hasta la actualidad por el matemático Wantzel, quien aseveró la imposibilidad de la trisección de un ángulo con el compás y la regla. El matemático circense, sin embargo, aseguró ayer en Erandio (Vizcaya) haberlo conseguido en sólo dos días. La vida te da sorpresas, sorpresas te da la vida."

Amb els anys he perdut l'original de l'article del qual només em queda un retall de la imatge. Per sort tenia el text copiat.

La notícia no acaba aquí. Al juny del 2012 el dominical de La Vanguardia dedicava un article a Luis Raluy i encara s'insistia en el tema de la trisecció.

Article original