Els "sona": contes, geometria i nombres (1)

Al llibre Una historia de la proporción de Manuel García Piqueras (Nivola, 2013) fa un apunt sobre uns dibuixos que alguns "contacontes" africans fan al terra tot acompanyant la seva narració. El mateix autor els ha utilitzat en una altra obra més recent de caire narratiu: La supersobrina y el enigma del gran astrolabio (Nivola, 2016). Però en cap d'aquestes obres entra en profunditat en el seu anàlisi matemàtic. El podem, però, trobar en un article seu en el n. 78 de la revista Suma: Un atardecer en África y América o en les actes de les 15 JAEM de Cartagena on va fer un taller conjuntament amb A. Bueno i J.L. Muñoz: Sona: una herramienta didáctica para primaria y secundaria. Per tant, ja podeu endevinar que només faré que reexplicar els seus materials. El cas és que darrera dels sona hi ha una interessant problema matemàtic.

Però millor que comencem sentint conte i veient un d'aquests dibuixos, realitzats pel propi Manuel G. Piqueras.

El perro y el cazador

Si observem el dibuix final del conte i fem alguna petita deformació geomètrica trobarem que és una figura que es pot fer d'un sol traç envoltant els punts d'un rectangle de 4x3. Aquest tipus de dibuixos es diuen sona, en plural, i lusona en singular.

Lusona del conte

Dibuixat amb segments rectilinis

Eliminant "deconnexions"

Si ens hem fixat en el vídeo la línia continua del lusona comença en un punt extern al rectangle de punts, avança amb un angle de 45º fins a un altre punt extern on "rebota" i continua avançant amb un angle de 45º però en una altra direcció. Potser per explicar i estudiar el dibuix del lusona convé fer una mica "de neteja" en la quadrícula i afegir alguns punts exteriors que ens ajudin a fer el dibuix.

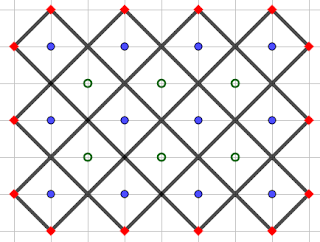Afegim els punts on la línia "rebota"

Eliminem els punts interiors

Podem veure ara una animació on es visualitza com sortint d'un punt i rebotant a les parets del rectangle que emmarca es pot dibuixar el lusona.

Investiguem sones sobre diferents rectangles?

• El rectangle de 4x6

Podem començar a dibuixar el nostre lusona per qualsevol punt. Però, en aquest cas, veurem que no hem aconseguit unir tots els punts (en els sona tradicionals implicaria no envoltar tots els punts interiors).

El que podem fer ara és tornar a començar des d'un altre punt qualsevol. Veurem que ara si hem completat tots els punts. Hem necessitat "dues voltes".

• El rectangle de 6x9

En un rectangle de 6x9 observarem que necessitarem "tres voltes" per completar el lusona.

• El rectangle de 5x5

En aquest cas per recobrir tots els punts ens calen 5 voltes.

•  I en general?

En aquest enllaç podeu trobar un applet en GeoGebra que permet experimentar sobre taulers de qualsevol de les mides entre 1 i 9 punts de costats. En aquest altre a més podreu trobar solucionats de forma dinàmica alguns casos particulars. Tots dos han estat dissenyats per Antonio Bueno.

Si anem estudiant casos diferents de forma sistemàtica podem construir una taula com aquesta:

No és difícil observar que la quantitat de voltes és el màxim comú divisor dels dos costats.

I a l'aula?

• Fer la investigació més o menys com s'ha explicat aquí.
• Un càlcul relacionar és esbrinar la quantitat de rebots necessaris perquè una trajectòria torni al punt inicial. Ja que s'han de "tocar" tots els punts exteriors en general hi hauria un rebot menys que el total de punts. Però això només es cert quan l'itinerari és únic, és a dir, quan els dos costats són primeres entre ells. Així que al total de punts li haurem de descomptar el total d'inicis i dividir aquest resultat entre la quantitat d'itineraris. Es pot comprobar que tots els subitineraris d'un rectangle donat tenen la mateixa quantitat de rebots.

Rectangle de 6x9: (30-3)/3 = 9 rebots per trajectòria

• Intentar justificar perquè la quantitat d'itineraris es correspon amb el m.c.d.
• Investigar més sobre aquests tipus de dibuixos: a quina zona de l'Àfrica es fan servir, descobrir altres exemples de dibuixos i contes relacionats.
• Fer un conte propi i dissenyar el seu lusona.

• Ampliar la investigació. Un exemple que proposa el propi Manuel García Piqueras als seu article de Suma n.78 convida a col·locar "miralls" en els punts interiors dels rectangles. De fet cal aclarir que amb la deformació del primer lusona que hem presentat hem fet una mica de trampa perquè hem acabat connectant punts que no ho estaven abans. Si ho mirem bé el lusona del gos i el caçador tenia dos miralls que desviaven la línia i eliminaven un possible creuament.

La proposta d'investigació ara és estudiar com col·locar els miralls per convertir un lusona de més d'un recorregut en un altra d'una sola trajectòria i descobrir quin és el mínim de miralls necessaris per un rectangle determinat. També es pot estudiar la col·locació de miralls que augmentin el total de recorreguts.

Aquest lusona amb un mirall convenientment col·locat tindrà un sol itinerari. Es pot col·locar en qualsevol lloc els miralls? Si no és així... on s'han de posar?

Al mateix lusona un mirall col·locat en una altra intersecció augmenta en un els itineraris

• Una segona línia d'investigació del mateix article consisteix en estudiar combinació de sona i quins efectes tenen en la quantitat de recorreguts.

Adossar aquests dos lusones de un i dos itineraris produeix un de tres

Els dos mateixos lusones adossats pel vèrtex produeixen un sol itinerari

• Un applet que juga amb aquests "rebots" però amb una taula de billar i que es pot utilitzar també a primària és Proportion Playground.

Continuació de l'article a Els "sona": contes, geometria i nombres (2)