Al concurs del Fem Matemàtiques del 2020 un dels problemes estrella va ser el del Loop de loops que va aparèixer, amb diferents variants, a les tres categories principals. És un problema prou ric i sobre el que es poden fer diferents enfocaments. Posteriorment, al Banc de Recursos del Fem Matemàtiques li han dedicat dos articles d'anàlisi (1 i 2) amb exemples de solucions d'alumnat i propostes d'avaluació. Vegem un dels sues plantejaments i que es correspon amb el que es va proposar a 1r d'ESO:
- Agafem un dau i el tirem cinc vegades. Anotem ordenadament es resultats. Per exemple 2,4, 3, 2 i 5.
- Sobre una quadrícula fem un segment de tantes unitats com el primer resultat. Girem 90º a la dreta i fem un altre segment d'una longitud. Girem 90º a la dreta... i així fins a dibuixar els cinc segments.
- Des del punt on hem acabat girem 90º en el mateix sentit i repetim el procés.
- I continuem tantes vegades com siguin necessàries fins que tornem al punt d'inici i tanquem el loop. En el nostre exemple cal fer-ho dues vegades més.
 |
| La sèrie 1-4-5-3-3 (90º) necessita 4 iteracions per a tancar el loop |
Abans d'entrar en la nostra proposta, pot ser interessant fer un incís i mirar-ne una altra, molt ajustada per a primària i principis de l'ESO, que vaig sentir a Marc Caelles (@caellesmarc) en una presentació d'Innovamat. Es tracta de reduir la sèrie de nombres a tres (no tenen perquè ser les tirades d'un dau) i amb un angle de 90º. L'activitat es basa en fer diferents loops, classificar-los segons la forma i buscar la pauta numèrica que fa que s'obtingui un tipus de loop o un altre. A continuació teniu un enllaç a un applet de GeoGebra que us permetrà experimentar. La resposta a la investigació la trobareu a la xerrada d'en Marc (minut 52).
 |
| Enllaç a l'applet |
Anem ara a centrar la nostra investigació en dues preguntes:
- Podem saber si un loop tancarà o no abans de dibuixar-lo?
- Afecten les mides dels segments al tancament?
Ens hi posem?
Farem totes les activitats amb longitud de segments obtingudes amb daus. D'aquesta manera no augmentem la quantitat de longituds a estudiar i treballarem sempre amb nombres naturals.
Tancarà o no tancarà?
Com sempre el millor és anar experimentant i prenent dades, més o menys ordenades, dels resultats que anem obtenint.. Una bona ajuda pot ser fabricar-se un programa. Scratch o Snap són ideals. Aquí en teniu un exemple millorable. Primer us demanarà la quantitat de daus (de segments) i després l'angle de gir en graus. Prement la tecla "espai" podreu anar fent loops. Un so i un missatge detectaran el tancament del loop (tot i que el programa no sempre detecta el tancament).
Podem començar provant diferents quantitat de daus amb un angle determinat, per exemple 90º. Algunes observacions possibles poden ser aquestes.
Després podem seguir amb altres angles. Només afegirem un altre exemple: una taula més: 60º.
Si continuem experimentant podrem començar a fer les nostres primeres conjectures. Per exemple:
- Excepte en alguns casos el resultats dels daus no influeix.
- Sembla que influeix quan la quantitat de daus multiplicada per l'angle fa un múltiple de 360 (4·90, 8·90, 6·60)
- La quantitat d'iteracions necessàries per tancar varia però s'intueixen algunes relacions de divisibilitat. Per exemple, amb 90º es poden endevinar per si la quantitat de daus és parell o senar. I amb 60º algunes quantitats de segments tenen les mateixes iteracions: 5-7, 2-4-8, 3-9.
Un cop tenim unes primeres conjectures hem d'anar fent proves noves per confirmar-les, depurar-les o descartar-les. I així, de mica en mica, podem arribar a una fórmula com la següent, que ens dona les iteracions per a la majoria de casos (n és la quantitat de daus i α l'angle de gir).
Com afecten les mides dels segments?
Hem vist que, en general, no afecten i podem saber si el loop tancarà o no. De fet, només tenim un cas de dubte: quan el producte de la quantitat de segments per l'angle de gir és 360º o un múltiple d'aquest. Com sempre, una bona tècnica és reduir el problema. Estudiar alguns casos i cenyir-nos majoritàriament a que el producte sigui exactament 360º pot ser un bon començament. Anunciem ja, però, que en aquest cas no trobarem una solució general.
- Girs de 90º
Però, segons les mesures dels segments, hi ha casos ens els que sí es tanca. Amb quatre segments és molt fàcil pensar en el cas de l'obtenció d'un rectangle si les mides es repeteixen en la seqüència a-b-a-b.
Estudiem, en aquest cas, quan tancarà amb 8 segments. Especialment perquè ens donarà idees per a altres angles. Mirem aquest exemple:
Hem assenyalat amb colors diferents els segments que dibuixem caminant cap a l'est, cap al sud, a l'oest i al nord. Si hem d'acabar on hem començat tots els desplaçaments horitzontals s'han d'anular entre sí: els que van a l'est amb els que van a l'oest. I els verticals també: els que s'orienten al nord han de sumar tant com els que s'orienten al sud.
Així si tenim 8 segments a-b-c-d-e-f-g-h, el assignem un signe (positiu per a E i N i negatiu per a O i S) s'hauran d'acomplir les següents relacions:
a-c+e-g = 0 → a+e = c+g
-b+d-f+h = 0 → b+g = d+h
Podem estendre aquesta idea a altres quantitats de segments múltiples de 4.
- Girs de 60º
Hi ha casos que són fàcils:
- quan els sis segments són iguals
- el cas en què els tres primers segments són iguals als tres segons (en mida i ordre).
 |
| El segment més gruixut és el primer i es comença en direcció est. |
Però també trobarem casos més irregular. Per exemple aquest en el què tots els segments tenen mesures diferents.
 |
| Posem amb el mateix color els costats paral·lels |
El que és curiós és que es pot trobar una relació numèrica relativament senzilla entre les mesures. Posem quatre exemple per si ho voleu pensar. La manera d'agrupar-los i els nombre en negreta són una pista.
1-5-3 | 4-2-6
4-6-3 | 3-7-2
5-7-4 | 4-8-3
6-4-4 | 4-6-2
1-5-3 | 4-2-6 → 5-3-4 | 2-6-1 → 3-4-2 | 6-1-5 → etc.
Gràficament la idea és que busqueu una relació entre cada grup de segments. I que el valor del que és més gruixut "pesa més" que els dels altres dos del mateix color.
Curiosament la condició insinuada és "necessària, però no suficient". Si heu descobert la relació veure que aquesta sèrie de segments acompleix la relació però el polígon no es tanca.
 |
| 6-3-2 | 1-6-1 |
Cal que s'acompleixi una altra relació entre els dos parells de costats de l'hexàgon marcats amb colors.
 |
| Les dues condicions "il·lustrades" |
Al final de l'article trobareu les solucions i un enllaç a una demostració del per què d'aquestes relacions.
- Girs de 45º
 |
| a-b-c-d-a-b-c-d https://www.geogebra.org/m/bpnepwjb |
- Girs de 72º
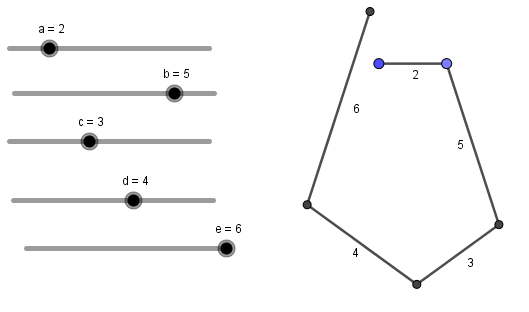 |
| https://www.geogebra.org/m/tud3dznv |
- Gir de 30º
 |
| https://www.geogebra.org/m/bb6gbtwa |
Una investigació a fons ens permetrà descobrir que s'han d'acomplir quatre condicions simultànies i que tenen una bonica simetria. També guarden una certa relació d'aparença amb el cas de 60º.
Aquests relacions costen molt de trobar per tempteig. Aquí les hem esbrnat utilitzant trigonometria. Al final de l'article trobareu un enllaç que les justifica. Sense descomptar els casos invertits, cíclics o que hem qualificat de trivials, i amb nombres de l'1 al 6, hi ha 443 556 solucions.
- Fem resum de la segona pregunta
- Quan la quantitat de segments és senar sempre es pot fer el polígon regular. Probablement és l'única solució.
- Quan la quantitat de segments és parell sempre podem fer el polígon regular o aquells en que la primera meitat de segments coincideix, un a un, amb la segona meitat. Per exemple, per a 6 segments: a-b-c-a-b-c.
- Per a determinats angles podem trobar solucions més irregulars quan els costats acompleixen un conjunt de relacions. Podem sospitar que només passa amb angles de 30º i 60º. Les raons no les hem insinuat fins ara, però tenen a veure amb la racionalitat del seu sinus i cosinus respectivament.
I a l'aula?
- Les propostes del Fem Matemàtiques són perfetament aplicables en els seus cursos assignats des del concurs i les tenim ben explicades en els enllaços que hem posat del Banc de Recursos.
- La de tres segments amb angles de 90º d'Innovamat (també enllaçada abans) és magnífica per a primària.
- Des del blog de Dan Meyer can organitzar un concurs artístic amb loops de 90º que pot donar bones idees per afegir un plus a l'activitat.
- El cas general de veure quan tanquen o no tanquen depenent de la quantitat de segments i de l'angle és perfectament aplicable a secundària. Pot ser molt interessant fabricar algun programa per a fer els dibuixos automàticament.
- Hi ha programes fets. Aquest, de The Mathenæum, construeix amb segments de longituds 1, 2, 3... n.
- El cas específic quan la quantitat de segments n coincideix amb la divisió de 360/α és abordable en general. Especialment els casos de 90º o, per altres angles i amb quantitats parells de segments amb mitges seqüències repetides. El cas de 60º es pot experimentar i amb una bona construcció de taules, recollint dades ordenadament, les dues relacions necessàries són "descobribles". Potser s'han de donar pistes. No cal justificar les relacions.
- També podem investigar quan tancarà o no si, a més de canviar la longitud dels segments, podem canviar cada vegada l'amplitud de l'angle. Només haurem de canviar n·α per la suma dels angles de gir.
- Si volem justificar els casos específics del punt anterior, en quant a les condicions per tancar o no tancar loop a la primera, cal l'ús de la trigonometria. Ho explicarem a continuació. Potser un treball interessant per als més grans.
Respostes i demostracions
- Relacions entre costats per 6 segments i gir de 60º.
Només es tancarà un polígon directament si les relacions entre els costats són les següents:
Per a demostrar-ho hem de considerar que, si agafem com a punt se sortida el segment a en sentit Est i agafant la seva direcció com a horitzontal, el total de les distàncies horitzontals recorregudes en direcció E i O han de ser iguals i anul·lar-se entre sí. I que ha de passar el mateix amb els desplaçaments verticals: que el que es camini cap al S es compensi amb el que es camini cap al N. D'aquesta manera acabarem on hem començat i el polígon es tancarà. Per a calcular aquests desplaçaments necessitarem de triangles rectangles auxiliars, per a fer les projeccions dels desplaçaments, i fer els càlculs trigonomètrics associats.
- Demostracions
Per no carregar l'article us proposem mirar els documents respectius en format pdf:

















Cap comentari:
Publica un comentari a l'entrada