Fa molts anys em va caure a les mans un text de Josep Pla titulat "El vent de garbí i la tramuntana". Un dels seus apartats es titulava Explicacions científiques. En ell, per primera vegada, vaig trobar la referència a les formes el·líptiques de la badia de Roses. En Pla comenta un escrit de Frederic Macau (1917-1970) on hi ha tot l'estudi matemàtic pertinent, les seves justificacions geològiques i climàtiques i un petit teorema que ell mateix anomena "Teorema de l'Empordà"
En el text de Pla es diu:
És absolutament obvi que el perfil del golf de Roses és la forma més admirable, més impressionant, d'una més excelsa bellesa, més inoblidable de l'Empordà. (../..) És una forma de gran bellesa, produïda per la naturalesa en cru, que mai, potser, l'obsessió artística no arribarà a dibuixar una forma que s'hi assembli. (../..) El senyor Macau se l'ha mirada amb ulls d'artista i de científic -n'ha donat una informació de gran categoria. Una visió superficial del golf fa aparèixer una forma el·líptica geomètricament perfecta. És una el·lipse com si hagués estat traçada amb un tiralínies per un delineant expertíssim. Però d'el·lipses, n'hi ha dues: una de petita, del cantó de Roses, i una de més llarga del cantó de l'Escala. L'eix de l'el·lipse de la banda de Roses coincideix en direcció i situació amb la perllongació dins del mar de l'últim tram del Muga. L'eix de l'el·lipse de la banda de l'Escala, coincideix, encara que no tan exactament, amb la direcció i la perllongació del penúltim tram del Fluvià".
El text continua donant més detalls matemàtics recollits de l'escrit de Macau on, a més, hi ha alguna referència a la proporció àuria. Si el voleu llegir es titula "L'Alt Empordà geometritzat per la Tramontana".
 |
| Imatge original del text de Frederic Macau |
La segona vegada que em vaig trobar amb una referència a l'estudi de Macau va ser a l'exposició de Perejaume "Maniobres de Perejaume", a l'any 2014.
La tercera, va ser a la revista NouBiaix, al n. 79, també de 2014, on Lluís Sabater, de l'IES Llança, feia tot un estudi amb GeoGebra de les propostes de Macau. L'article es titulava El Teorema de l'Empordà (de F. Macau) vist amb el GeoGebra.
 |
| Enllaç a la construcció de Lluís Sabater |
Ja avanço que, amb tots el meu sincer respecte per l'obra de Macau, aquestes coses no me les pren mai del tot seriosament. Per una banda, la natura "no és exacta". Per una altra, nosaltres fem passar les línies per on ens va millor. Quantes vegades hem vist obres que troben tot de proporcions àuries dibuixant rectangles auris amb aproximacions triades a conveniència?
 |
| Aquí em deixo un colze, aquí un tros de mà, aquí... |
 |
| Una sola el·lipse posant els límits entre l'entrada de Roses i la zona d'Empúries |
 |
| Una hipèrbola posant els límits entre La Muga i Empúries |
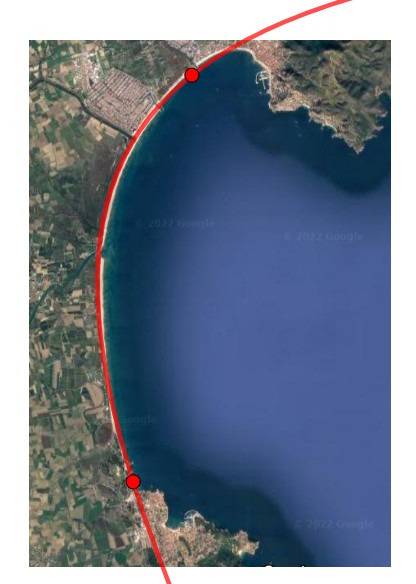 |
| Una paràbola entre el Port de Sta. Margarida i Empúries |
Una altra possibilitat d'exploració, és intentar endevinar on estan els focus de les el·lipses i després comprovar el nostre grau d'encert. Ens pot ajudar a fer-nos una idea de la posició dels focus en relació a l'excentricitat de les el·lipses.
I a l'aula?
- Aquesta activitat, com s'ha vist, s'ha proposat d'una manera molt senzilla: una primera experimentació amb l'eina "Cònica que passa per cinc punts" de GeoGebra. Una segona relacionada amb els focus de l'el·lipse. Crec que està bé per familiaritzar-se, en un context curiós, amb les còniques sense fer un treball analític o geomètric exhaustiu. També ens pot ajudar a veure que, sovint, és difícil discernir visualment si un arc és d'el·lipse, hipèrbola o paràbola (o catenària, que, tot i no ser una cònica, és freqüent en construccions).
- Es pot ampliar l'activitat a partir de la lectura de l'article de Frederic Macau i de la demostració del Teorema de l'Empordà proposada per Lluís Sabater. I debatre sobre la hipòtesis dels dos arcs d'el·lipse proposats, la recta de tangència i la que uneix els centres de les el·lipses seguint la línia de la Tramuntana, les orientacions dels eixos petits amb el rius, les justificacions geològiques i climàtiques... I parlar sobre la versemblança de les seves teories.
- De fet, és una oportunitat per parlar, d'aquestes qüestions matemàtiques o pseudomatemàtiques. En podem trobar altres exemples en la literatura. I molt especialment relacionades amb la proporció àuria, com també passa en el text de Macau que la troba en la relació entre les longituds dels dos semieixos grans de les dues el·lipses (13,9 km : 8,6 km = 1,616...).
 |
| El Delta de l'Ebre en una el·lipse? |



Cap comentari:
Publica un comentari a l'entrada