Ampolles, soldats, monges... Un mateix problema. Diferents versions

Al llibre "Problemas y Experimentos Recreativos" Iàkov Perelman (1882-1942) plantejava un problema sota el títol Els ardits de la guàrdia. A la presentació ja anunciava: "Aquest problema té moltes variants. En donem una". I, a continuació, explicava la següent història:

"La tenda de campanya del cap la custodiava una guàrdia allotjada a vuit tendes. Al principi a cadascuna d'aquestes tendes hi havia tres soldats. Després es va permetre que els soldats d'unes tendes poguessin anar a visitar als altres. I el cap de la guàrdia no imposava sancions quan en entrar a les tendes trobava en unes, més de tres soldats i en altres, menys. Es limitava a comprovar el nombre de soldats que hi havia a cada fila de tendes: si a les tres tendes de cada fila hi havia en total nou soldats, el cap de la guàrdia considerava que tots els soldats eren presents.

Els soldats se'n van adonar i van trobar la manera de burlar-se del cap. Una nit van marxar quatre soldats de la guàrdia i la seva absència no va ser notada. La nit següent se'n van anar sis, que tampoc van patir càstig. Més tard els soldats de la guàrdia fins i tot van començar a convidar els altres a visitar-los: en una ocasió en van convidar quatre, en una altra, vuit, i una tercera vegada, tota una dotzena. I totes aquestes astúcies van passar desapercebudes, ja que a les tres tendes de cada fila el cap de la guàrdia comptava en total nou soldats. Com se les componien els soldats per fer això?"

Resumint el problema: tenim un quadrat de 3x3 en què la casella central interior no compta.  Podem posar a cada casella tants soldats com vulguem mentre es puguin comptabilitzar nous soldats per banda. Inicialment hi ha 24 soldats: Com hem de distribuir els soldats perquè el cap de la guàrdia no s'adoni de res en dies què n'hi ha 20, 18, 28, 32 i 36 soldats?

La proposta per a investigar va una mica més enllà: quines són les quantitats mínima i màxima de soldats que podem tenir? Entre aquestes quantitats, es poden obtenir totes les altres? I si en comptes de 9 soldats per banda, són n? Quines seran les quantitats límit? Podem descriure algun patró o mètode per obtenir totes les solucions possibles?

A banda de la investigació us presentarem, a continuació, algunes variacions del problema: versions més antigues històricament o plantejades amb dos pisos.

Continuem?

Investiguem el problema

Potser, inicialment, la situació sembla paradoxal. Però de seguida que comencem a fer proves, veiem que la clau és jugar amb la quantitat de soldats que posem a les caselles centrals de cada costat i en la que posem a les caselles que fan cantonada. En aquestes, cada soldat és comptat en dos costats i, a les centrals, només en un.

Així, si volem tenim menys soldats de l'habitual i que es continuï comptant nou soldats per costat, els haurem d'acumular a les cantonades. I si en volem tenir més, a les centrals.

De vegades, ens posem una autolimitació: no deixar caselles buides. Però a l'enunciat no diu res sobre aquest tema. Tenint en compte la possibilitat de no posar soldats a certes cel·les veurem, amb una certa facilitat, els dos casos extrems:

• no posar-ne cap a les cantonades i obtenir un màxim possible de 36 soldats.
• no posar-ne cap a les centrals i obtenir un mínim de 18.

La solució mínima pot tenir diferents distribucions a les cantonades

Si ja tenim els límits marcats, cercar les altres solucions no és complicat: les del problema i d'altres. El problema de Perelman només ens demanava algunes de les solucions parells. No és difícil obtenir totes, posant sempre a la casella central de cada costat una mateixa quantitat: 0, 1, 2... i fins a 9.

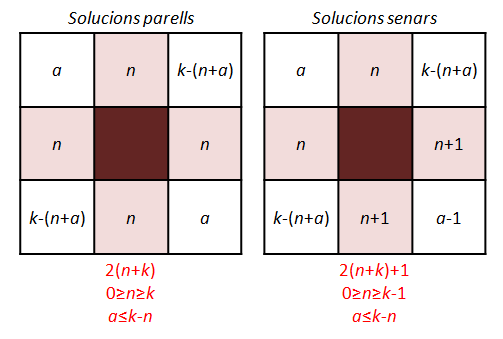
Aquí hem posat totes les solucions amb zero soldats a dues de les cel·les cantoneres (cantonades amb 9 i 0). Però n'hi ha més: 8-1, 7-2, 6-3 i 5-4. Si diem n a la quantitat de soldats que posarem a la casella central i a a la que posem a una de les cantonades, la distribució completa i el total obtingut tindran la següent forma algebraica:

Ens queda trobar les solucions amb totals senars. Només cal experimentar una mica més i, probablement, trobarem un nou patró de distribució que ens les donarà.

Com a les solucions parells, el que importa és el que posem a les caselles centrals, mentre les cantonades completin nou per costat, no hi ha problema. Ara la forma algebraica de les distribucions serà la següent:

Generalització

Podem variar la quantitat de soldats a comptar per banda. Anomenem-la k.

• El mínim sempre s'obtindrà d'acumular-los tots entre dues cantonades. Si la quantitat a comptar per costat és k el mínim total serà 2k.
• El màxim total s'aconseguirà no posant cap soldat a les cantonades i col·locar-ne k a cadascuna de les caselles centrals. El màxim total serà 4k.
• Entre aquest mínim i aquest màxim es podran obtenir totes les quantitats seguint patrons com els que hem vist abans.

Altres versions "d'un pis"

Si volem posar a prova les descobertes que hem fet podem fer-ho amb altres versions del problema.

• E.I. Ignatiev. Anteriorment a Perelman, Ignatiev va publicar, a l'any 1908, un llibre que aquí es va traduir com "En el reino del ingenio". El problema 69, titulat, El conte sobre el príncep Ivan i Kaschei l'Immortal, que sabia comptar només fins a deu és similar en tot, però amb una història molt més llarga. Pot ser una bona idea per introduir l'activitat a classe amb una narrativa més entretinguda. Però tenim altres dos que varien una mica. El 67 (Disposició de sentinelles) manté un total constant i demana diferents distribucions. El 68, en un context diferent, és com el dels soldats, però amb altres quantitats. No el posem aquí ara perquè presentarem la versió en què es va inspirar.

 Problema 67. Disposició de sentinelles

Al llarg de les parets d'un bastió quadrat calia posar 16 sentinelles. El comandant els va distribuir  amb 5 persones a cada costat.

Després va venir el coronel i, no satisfet de la posició dels sentinelles, va donar l'ordre de distribuir soldats de tal manera que a cada costat estiguessin 6. Després del coronel va arribar el general, es va enfadar amb el coronel pel seu ordre i va distribuir els soldats de manera que van quedar 7 persones per cada costat.

Quines van ser les distribucions en els dos darrers casos?

• Claude-Gaspard Bachet de Méziriac (1581-1638). Va ser autor del llibre Problèmes plaisants et délectables qui se font par des nombres, publicat al 1612. Allà hi trobem una de les primeres, sinó la primera, versions impreses d'aquest problema. El problema del "Propietari burlat" d'Ignatiev recull aquest de Bachet. 

"Un bon burgès va fer al seu celler un armari de nou caixes disposades en un quadrat; la caixa del mig estava destinada a rebre les ampolles buides resultants del consum de seixanta ampolles plenes, que va col·locar a les altres vuit caixes posant sis ampolles a cada caixa cantonera i nou a cadascuna de les altres caixes.

El seu servent va treure primer quatre ampolles que venia, i va disposar les ampolles restants de manera que sempre n'hi haguessin vint-i-una a cada costat de la plaça. L'amo, enganyat per aquest arranjament, va pensar que el seu criat només havia transposat ampolles, i que sempre n'hi havia el mateix nombre. El criat va aprofitar la senzillesa del seu amo per treure quatre ampolles més, i així fins que ja no es va poder treure quatre sense que el número vint-i-un deixés d'estar a cada costat de la plaça. Li preguntem com ho va fer cada cop i amb quantes ampolles va fer mal al seu amo.”

Cal dir que, tant Bachet com Ignatiev,  només donen les solucions sense caixes buides i que guarden una certa simetria com la de la disposició inicial.

• Luca Pacioli. De viribus quantitatis (Del poder dels nombres). En aquest manuscrit del 1500 apareix una versió senzilla del problema. Tenim vuit monges, una a cada cel·la, fent un total de tres monges per costat. Com les podem reordenar perquè hi hagi quatre per costat?

• Sergio Belmonte. El triangle de les Bermudes. En Sergio, professor mag-matemàtic col·laborador del MMACA, presenta el joc en forma de truc de màgia i basat en un triangle en comptes d'un quadrat. No entrem en els detalls perquè ho fa ell mateix en el seu blog Magia y matemáticas. A més inclou enllaços amb altres referències al problema. 

Imatge procedent del blog Magia y matemáticas

Versions de "dos pisos"

Els dos grans creadors de problemes Sam Loyd (1841-1911) i Henry Dudeney (1857-1930) també es van inspirar en problemes existents anteriors. I, fins i tot, s'inspiraven l'un en l'altre (per dir-ho suaument). Tots dos tenen problemes com el que hem plantejat inicialment, però jugant amb edificis de dues plantes. A tots dos els agradava vestir els problemes d'històries més o menys complexes.

La versió de Sam Loyd ja la vam proposar en un article anterior d'aquest blog: Loyd i les monges dels Pirineus. Si voleu la versió completa de l'enunciat la podeu trobar en el problema 46 d'aquesta versió del llibre "Los acertijos de Sam Loyd".

Bàsicament, ens parla d'un convent amb dues plantes de vuit habitacions cadascuna. La Mare Superiora ha donat algunes ordres sobre com s'han de distribuir les monges a les habitacions:

• Totes les habitacions han d'estar ocupades.
• A una planta hi ha d'haver el doble de monges que a l'altra.
• S'han de comptar 11 monges per costat entre les tres habitacions d'un pis i les tres de l'altre.

En un moment donat són segrestades nou monges. Les altres es reordenen de forma que la Mare Superiora no nota res. Es demana quantes monges hi ha al convent.

Ara es tracta de trobar dues distribucions: una amb n monges i una altra amb n-9... però sense saber el valor d'n. Loyd no fa cap comentari sobre la resolució, només es limita a donar els resultats.

La versió de Dudeney, publicada al llibre "Los acertijos de Canterbury" (1907) i que donem completa, és pràcticament clavada a la de Loyd. Només afegeix una condició: a cap habitació hi pot haver més de tres pelegrins.

"L'enigma dels pelegrins. Un dia, quan els monjos estaven asseguts dinant, l'abat va anunciar que aquell matí un missatger havia portat la notícia que uns quants pelegrins estaven pel camí i que requeririen la seva hospitalitat. "Els posareu", va dir, "al dormitori quadrat que té dos pisos amb vuit habitacions a cada pis. Hi ha d'haver onze persones dormint a cada costat de l'edifici, i el doble al pis superior que al pis superior. Per descomptat, totes les habitacions han d'estar ocupades, i ja sabeu la meva regla que no poden haver-hi més de tres persones a la mateixa habitació".

Us dono un plànol de les dues plantes, des del qual es veurà que a les setze estances s'hi accedeix per una escala de cargol al centre. Després que els monjos havien resolt aquest petit problema i disposat l'allotjament, van arribar els pelegrins, quan es va comprovar que eren tres més del que es deia inicialment. Això va obligar a reconsiderar la qüestió, però els monjos astuts van aconseguir superar la nova dificultat sense trencar les regles de l'abat. El punt curiós d'aquest trencaclosques és descobrir el nombre total de pelegrins."

Dudeney sí que dona alguna explicació més sobre les possibles solucions. De fet, ens en fa un llistat de totes les solucions possibles. La seva limitació de no deixar habitacions buides i no excedir de tres pelegrins, ajuda a acotar les respostes.

A continuació teniu un aplicatiu que us permetrà fer proves interactivament.

Enllaç al programa

I a l'aula?

• La versió presentada inicialment (9 per costat) és, segurament, la millor per plantejar inicialment a l'aula, la més abastable, i prou rica a la vegada, per presentar a l'aula i fer una cerca exhaustiva de totes les solucions. Deixem a la imaginació de mestres i professorat buscar contexts menys carrinclons. Si bé també es pot considerar plantejar els contextos originals constatant que són problemes històrics i situant els seus orígens.
• La generalització no cal plantejar-la algebraicament. A primària i als inicis de l'ESO es poden fer directament descripcions retòriques dels càlculs i les condicions. Si es fa així, també és una oportunitat per anar introduint el llenguatge algebraic.
• Pot ser ben curiós fer un passeig històric per algunes de les versions anteriors del problema