Comptem sobre un filera de daus

 Us convidem a fer el següent experiment:

• Agafeu molts daus. Per exemple, vint. El tireu tots a la taula i feu una filera, també de forma aleatòria, amb tots ells.

• Mireu els punts del primer dau i compteu fins tants daus com indica el nombre.

• Des d'aquest nou dau repetiu la forma de comptar... i aneu fent fins que arribeu a una quantitat des de la que ja no podeu seguir perquè no teniu tants daus com indica la darrera quantitat. Elimineu de la filera aquests daus sobrers. Si heu arribat justos no cal eliminar res.

• Ara elimineu el primer dau de tots, el que heu fet servir per iniciar el comptatge.

• Repetim la manera de comptar des del segon dau. Quina és la sorpresa? Que segurament acabareu al mateix dau que abans!

Però encara podem tenir més sorpreses. Sense anar més lluny, amb la seqüència que hem utilitzat com a exemple, podem repetir el procés de treure un dau i fer el comptatge 12 vegades més sense que canviï el dau final en el què acabem. És a dir, en total haurem pogut treure 13 daus.

Si no teniu daus a mà podeu experimentar amb aquest applet.

No sempre tindrem tanta sort. Aquí teniu una sèrie de 15 daus que al primer dau que traiem ja ens trobem amb un final diferent.

I a continuació dos exemples amb 10 daus. En un no es pot treure cap dau i a l'altre es poden treure tots.

No es pot treure cap dau

Es poden treure tots els daus

Ja tenim servida la situació. Ara toca fer-se preguntes:

• Per què moltes vegades es coincideix en un mateix final?
• Hi ha condicions que faciliten la coincidència?
• De que depèn la quantitat de daus que podré treure?

Investiguem?

Hem vist un exemple, amb 10 daus inicials, en el què podem treure entre 0 i 9 daus. En general amb n daus sempre podrem treure entre 0 i n-1 daus.

Per què hi tantes coincidències en els finals?

Ataquem ara la primera pregunta que ens havíem fet. La resposta la podem veure si marquem visualment alguns exemples. Per exemple, a la imatge veiem els comptatges amb una filera de 20 daus. A la primera jugada s'eliminen dos del final i dels 18 que queden podem eliminar fins a 13 primers daus mantenint la coincidència final.

Són fàcilment observables certes línies horitzontals de coincidència. Per exemple a les files 11 i 16. Si un comptatge passa pel dau número 11 de la fila original, i que té una puntuació de 5 [anotarem 11(5)],  seguirà el mateix camí final 16(2)-18(3). I a la fila 11(5) s'hi arriba per dues vies: des de 5(6) i des de 10(1). Però a 10(1) arribem des de... En el moment que hi ha una coincidència de "dau de pas" entre dos camins la via continuarà el mateix recorregut i, en conseqüència, tindrà el mateix final.

Podem mirar aquest "mapa" d'una jugada amb 50 daus dels que s'eliminen 2 a la primera jugada i dels 48 que en queden podem arribar a eliminar fins a 42. Les línies horitzontals de coincidència són molt clares.

 

De què depèn la quantitat de coincidències?

Un cop vist per què es produeixen aquestes coincidències finals ens poder demanar quines circumstàncies afavoreixen que hi apareguin més. Dit d'una altra manera: en quines circumstàncies podrem eliminar una quantitat major de daus.

A continuació teniu un applet per a experimentar. En primer lloc us demanarà la quantitat de daus que voleu que tingui la vostra filera. Veureu una "llista" amb les tirades obtingudes i la llista de llocs finals, d'on s'acaba, fins que s'arriba a un final diferent. "Daus trets" us dirà quants daus s'han pogut eliminar.

Per poc que experimenteu podreu fer algunes observacions:

• la quantitat de coincidències finals augmenta a mesura que ho fa la del total de daus de la fila. Això dit així sona a perogrullada. Però ho podem matisar dient que la proporció de coincidències finals respecte a la quantitat de daus inicials de la fila va augmentant progressivament. Hi haurà un percentatge de coincidències superior amb 50 daus que amb 10.
• si els resultats de les tirades són baixos hi haurà més coincidències. Dit d'una altra manera, les tirades curtes (com 1, 2 o 3) afavoreixen l'aparició de coincidències.

Si ho mirem totes dues observacions tenen molt de sentit: quant més daus tinguem i resultats més petits més fàcil serà que hi hagi camins coincidents en algun punt.

Quants daus podrem treure per a una quantitat de daus donada?

No és molt directe calcular aquesta probabilitat, però sí que podem experimentar. I millorar la nostra capacitat d'augmentar la quantitat d'experiments fent servir algun simulador informàtic. Així podem trobar una mitjana de daus eliminables per a una quantitat n que formen la filera. Aquí hem utilitzat un applet fet amb Snap, que ens permet determinar la quantitat d'experiments i la quantitat de daus de la fila. (Podeu revisar el codi per si hi trobeu alguna errada i així esmenar-la). Fent 10 000 experiments per a cada quantitat de daus, des de 5 a 100 i de cinc en cinc, els resultats obtinguts han estat aquests:

Podem veure com el resultat es va tornant més lineal a mesura que augmentem la quantitat de daus.

Si observem el creixement de la proporció entre la quantitat de daus eliminables i la inicial observarem un creixement més logarítmic.

El comptatge de Kruskal

Aquesta experiència amb daus és un exemple més del que es coneix com a comptatge de Kruskal i que s'utilitza sovint en efectes de màgia matemàtica. En aquest blog ja en vam parlar un parell de vegades amb uns exemples sobre texts. En un cas jugàvem amb un poema de Joan Brossa en el qual, triant una paraula qualsevol de la primera estrofa i passant d'una paraula a una altra segons comptant segons la quantitat de lletres, sempre s'arribava a una mateixa paraula clau. El poema era l'Sextina de la pau i la paraula final era "pactes"

Veure l'article

Pel 9-N vam repetir el joc amb un text de la Viquipèdia sobre Sissí (recordem que una de les opcions de vot era Sí-Sí) que acabava en la paraula "independència". (veure l'article)

Podeu ampliar informació sobre trucs de cartes amb aquest tipus de comptatge en aquestes enllaços:

• "La cuenta de Kruskal" al blog Magia y matemáticas de Sergio Belmonte (@magiaymates).
• Una versió en línia del truc explicat per Sergio Belmonte.
• Un altre article del truc a Ilusiones matemáticas.
• La mateixa activitat al web de l'NRICH: "Sociable cards"

 Una petita variant en la presentació de l'experiència

Una altra manera de presentar i estudiar l'experiment és fer, com abans, la fila de daus i el primer comptatge. Després, en comptes d'eliminar el primer dau, el tornem a tirar i comptem amb el nou resultat, per observar que acabem al mateix lloc, si més no, amb molta probabilitat. I ho repetim unes quantes vegades. A la imatge teniu un exemple amb 20 daus en el que, independentment del resultat del primer dau sempre arribem al mateix lloc.

Aquesta situació convida a fer-se algunes preguntes diferents. Per exemple, depenent de la quantitat de daus, quantes vegades la coincidència serà completa amb els sis primers resultats possibles, Una vegada més un programa amb Snap permet recollir resultats. A partir de 40 daus ens passarà més del 90% de les vegades.

Resultats per files de daus entre 10 i 100 amb 10 000 experiments per a cada cas

I a l'aula?

Com ja s'ha escrit en aquest blog en moltes ocasions, un dels objectius del treball en probabilitat és confrontar les nostres intuïcions inicials (sovint equivocades) amb l'experiència i el raonament sobre aquesta. Per tant, en un problema com aquest, no ens interessa tant el càlcul exacte de probabilitats, força complex en aquest cas, sinó veure que la sorpresa inicial té una explicació raonable i fàcilment comprensible. També és interessant la generació de noves preguntes.

A l'aula no podem fer la quantitat d'experiències necessàries per acostar prou la probabilitat experimental amb la teòrica. Però, si repartim la feina, en podem fer unes quantes. Si una parella d'alumnes fa cinc casos amb 20 daus, per exemple, i ho fem amb tot un nivell ens podem començar a fer una idea de per on van els trets. No és difícil generar llistes aleatòries amb un full de càlcul i després treballar-les com algunes de les taules mostrades abans. El "copiar-enganxar" estalvia molta feina. I una altra idea és guardar els resultats d'un any i anar acumulant les dades d'un curs amb les dels anteriors.

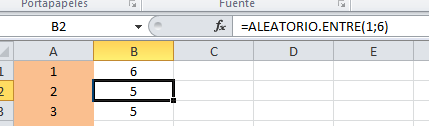Fórmula per simular un dau

Pot ser molt divertit investigar alguns textos a l'estil de la proposta sobre el poema d'en Brossa. La gràcia estar en que la paraula final tingui una mica de gràcia.

Un treball d'ampliació pot ser generar algun programa amb Scratch o Snap per fer les simulacions. Una millora curiosa podria plantejar-se com un truc de màgia equivalent al que hem enllaçat amb cartes: es genera una fila aleatòria de 40 o 50 daus i es demana a les instruccions que "a casa" es tiri un dau per començar a comptar. Després es pot marcar quin serà el dau d'arribada. A continuació teniu en exemple amb 40 daus.