De vegades hi ha patrons relativament senzills que, pel que sigui, no se t'acudeix buscar. La clau, com sempre, està en saber-se fer preguntes. Aquests patrons que presentem avui, en els què fins ara no m'hi havia fixat mai, els he trobat al llibre La matemática elgante (A.V. Zhúkov, P.I Samavol i M.V. Applebaum; Editorial URSS). Tots es basen en la taula pitagòrica de la multiplicació. I millor si la taula és "infinita". Els primers es basaran en la tria de quatre nombres que formin un quadrat seobre la taula. Després hi ha dos més basats en l'estudi de les sumes dels nombres que formen angles rectes i algunes diagonals. Abans d'entrar-hi és obligatori recordar un article, també referent a aquest tema, del Blog del PuntMat: "Patrons a les taules de multiplicar". Comencem.
- Quadrats amb els costats paral·lels a les vores de la taula
Triem quatre nombres que siguin els vèrtexs d'un quadrat col·locat "horitzontalment", que tingui els costats paral·lels als costats de la taula.
Podem descobrir una relació entre dues de les parelles de vèrtexs de cada quadrat. Quina és?
- Quadrats com els anteriors que tenen dos vèrtexs sobre la diagonal principal
A més de la relació anterior, en aquest cas, hi ha una propietat numèrica especial que s'acompleix considerant els quatre vèrtexs.
- Quadrats amb els costats paral·lels a les diagonals principals
Un cas relativament semblant al primer. Hem de trobar una relació entre dues parelles de vèrtexs.
- Suma dels nombres dels angles rectes de la taula (gnòmons)
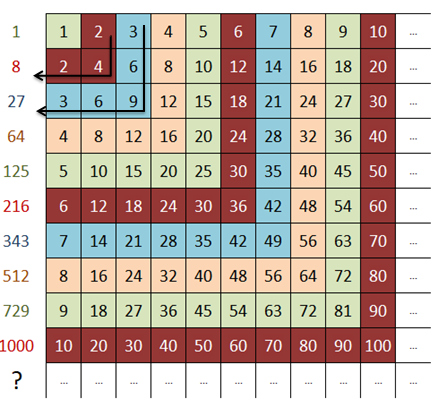
Si sumem els nombres que formen els gnòmons de la taula (podríem visualitzar-los com lletres L invertides), quin tipus de nombres obtenim?
- Suma dels nombres de les diagonals consecutives
Aquesta relació és una mica més complicada. Si sumem els nombres situats en les diagonals consecutives, marcades a la figura, podem trobar una sèrie numèrica curiosa. Podeu endevinar com segueix o identificar-la?
Us animeu a continuar investigant aquests patrons?- Quadrats amb els costats paral·lels a les vores de la taula
En aquest cas podem descobrir que el producte dels dos vèrtexs oposats per les diagonals, són iguals.
Aquesta propietat no és difícil de justificar. En aquest cas, i en els que venen, defugirem les demostracions de tipus algebraic. Per argumentar el perquè d'aquesta propietat no cal més que fixar-s'hi en un detall. Quan triem quatre vèrtexs amb aquesta regla, estem triant només quatre factors: dos per les dues columnes i dos per les dues files. En els vèrtexs oposats per la diagonal no repetim cap d'aquests factors, perquè triem els dos diferents de les columnes i els dos diferents de les files. D'aquí que els productes de cada parella de vèrtexs reuneixi els quatre factors i, en conseqüència, els productes seran idèntics.
- Quadrats com els anteriors que tenen dos vèrtexs sobre la diagonal principal
En aquest cas, a més, la suma dels quatre nombres serà sempre un quadrat perfecte.
 |
4+8+8+16 = 36 = 62
36+60+60+100 =256 = 142 |
Per justificar aquesta nova propietat, en Daniel Ruiz (
@druizaguilera), de Mallorca, em va donar la idea d'utilitzar la versió de la taula pitagòrica que fa visualitzar també les àrees de cada producte. Encara que, en certa manera i pel redimensionament de les caselles de la taula, perdem el quadrat original, que es "rectangularitza", podem fer una demostració visual "ad hoc" ben bonica.
No és gens difícil veure que el resultat final és el quadrat de la suma dels dos factors diferents que marquen les columnes i les files. En el cas de la imatge els factors són 6 i 8 el quadrat obtingut és (6+8)2=142. De fet, no es reconeix la demostració geomètrica del quadrat del binomi?
- Quadrats amb els costats paral·lels a les diagonals principals
La relació entre les parelles de vèrtexs és semblant a la que havíem vist pels quadrats anteriors. La diferència és que ara el que és igual és la suma.
Com abans, és una bona idea recórrer a la representació de la taula amb àrees per demostrar-ho. En aquesta animació fem un "mix": triem els nombres a una taula "normal", però sí que dibuixem els rectangles relacionats.
- Suma dels nombres dels angles rectes de la taula (gnòmons)
No és difícil veure que les diferents sumes van formant els cubs dels nombres naturals. La suma del gnòmon
n és
n3.
No és difícil comprovar algun cas amb materials com multilink. A la imatge teniu el cas de la suma del tercer gnòmon 3+6+9+6+3=27=33.
- Suma dels nombres de les diagonals consecutives
Observem primer quina sèrie obtenim.
Per a fer-nos una primera idea de la regularitat d'una sèrie, un bon sistema és observar les diferències successives entre cada parell d'elements de la sèrie.
És probable que uns ulls experimentats hagin reconegut la sèrie 3, 6, 10, 15, 21, 28... Són, efectivament, els
nombres triangulars. Però, en cas de no haver-la identificat, podem continuar cercant regularitats afegint columnes amb segones diferències, terceres... fins que trobem que la sèrie s'estabilitza (si és que ho fa, clar). En cas de voler buscar la fórmula la quantitat de diferències ens dona una pista del seu grau. En el nostre cas ho fa en la tercera diferència.
Si bé no és fàcil deduir una fórmula general, no ho és tant continuar la taula a partir dels patrons obsercats. Aquesta possibilitat està a l'abast de la gran majoria del nostre alumnat.
La fórmula general és:
També ulls experimentats poden haver reconegut la sèrie de sumes inicial, o la fórmula mostrada ara, com la dels
nombres tetraèdrics.
I a l'aula?
- Hi ha una primera proposta clara: promoure la cerca de patrons. Segons l'edat donarem més pistes o menys. També, segons l'edat demanarem argumentacions, o no, del perquè de cada relació. També podem estar atents a altres preguntes que poden sorgir a l'aula: sobre màxims i mínims, sobre fer un estudi similar a una taula additiva, subtractiva...
- Si per a algun curs superior esteu interessats en presentar les demostracions de les dues darreres sèries us recomanem adreçar-vos al llibre. Partint de la propietat de que els gnòmons sumen cubs, es demostra quina és la fórmula de la suma dels cubs d'n nombres consecutius. La demostració de les sumes de les diagonals és un bonic exemple de demostració per inducció.
- A la suma de diagonals apareixen els nombres triangulars i els tetraèdrics. Sobre nombres triangulars trobareu tres articles més en aquest blog: Triangles d'or, Fem-nos preguntes sobre la "persistència multiplicativa", on també hi surten els tetraèdrics, i El problema del testament del Nabab i la "resolució per síntesi".
 |
| Nombres triangulars (3a diagonal ) i tetraèdrics (4a diagonal) del Triangle de Pascal |
- També al Blog del PuntMat, a l'article Nombres amb forma (III), hi ha una proposta didàctica on apareixen tots dos tipus de nombres. Com no, al web NRICH (Triangle Numbers) ens proposen, entre altres activitats, un bonic patró amb els nombres triangulars sobre la taula pitagòrica.

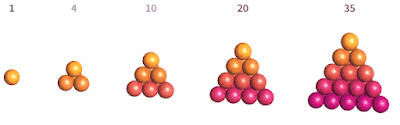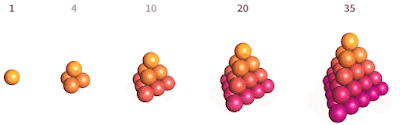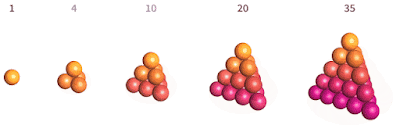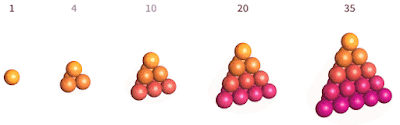


















Cap comentari:
Publica un comentari a l'entrada